Denumite în mod obișnuit ecuații integrante care implică funcția necunoscută sub semnul integral. Această definiție nu este foarte bun. Sub titlul „ecuațiilor integrale“ lucruri cunoscute, un pic ca unul de altul. De obicei, nu încercați să dea o definiție generală a ecuațiilor integrale, și sunt limitate la această listă cele mai importante clase de ecuații integrale.
Una dintre cele mai importante și bine studiată clasa de ecuatii integrale liniare este ecuația de Fredholm de tip II. Așa numita ecuație de forma:
(Spre deosebire de ecuațiile formei
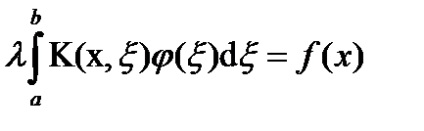
Dacă f (x) = 0, ecuația integrală este omogenă; în caz contrar - uniforma.
Funcția de două variabile reale se numește nucleul ecuației; parametru # 955; - evaluate complex. Nucleul este definit în caseta: a≤x, # 958; ≤b.
Nucleul ecuației (1) sugerează că
Termenul liber f (x) din ecuația (1) satisface
O inegalitate similară se presupune să dețină pentru funcția necunoscută # 966; (x).
In cazul in care (3) funcția f (x) este numit integrabile în (a, b). Nucleul ecuației integrale ar trebui să pătrat integrabilă în a≤x pătrat # 958; ≤b.
Fredholm a fost studiat cazul # 966; (x), f (x) - sunt continue pe [a, b], și
- în mod continuu în principal a≤x pătrat, # 958; ≤b. Evident, în acest caz, deține (3).
Ecuația integrală a formei (1) este o ecuație integrală cu o caracteristică slabă, dacă nucleul ecuației
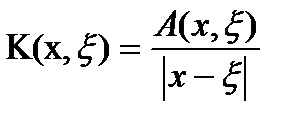
în cazul în care - o funcție continuă pentru a≤x, # 958; ≤b. În acest caz, ecuația este de asemenea, numit special sau singular.
În general, ecuația integrală se numește singular dacă fie a sau b sunt nelimitate; sau nucleul devine infinit la unul sau mai multe puncte ale intervalului.
Un caz special al ecuației (1) este o ecuație de forma:
Această ecuație se numește ecuația Volterra de tip II.
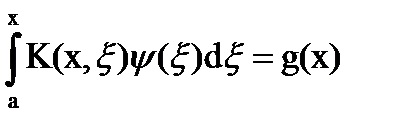
numit de tip Volterra I ecuația (nu vor fi luate în considerare).
Proprietățile ecuației integrale, este determinat de proprietățile nucleului sale soluții.
Pentru acest nucleu discută:
1) de bază transpus (5)
2) dual core (6)
Dacă ia numai valori reale, atunci.
Acest nucleu se numește:
Hermitian, în caz afirmativ,
critică, dacă deține (2) și integral ≠ 0,
continuă, în medie, în cazul în care
,
degenerate (sau separabile) dacă
.
Linear operatorul integral numit o transformare (cartografiere)
Ecuația (1) se poate scrie: (7)
Volterra ecuație integrală de tip II se reduce la o ecuație Fredholm pe (0, ∞), dacă introduceți un nou kernel
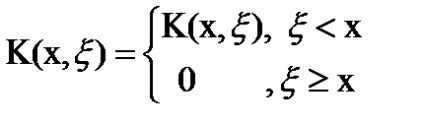
Soluția de rezolvare a ecuației integrale este o funcție # 966; (x), care, atunci când este substituită în ecuația aceasta atrage în identitate o rudă.
Exemplu. Verificați dacă soluția ecuației integrale
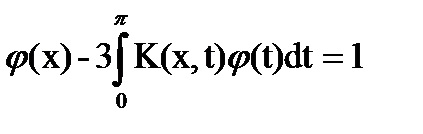
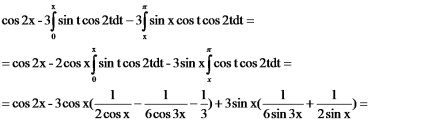
Integrați de părți:
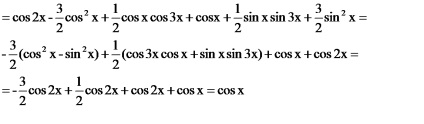
A: Funcția este soluția ecuației integrale.
exerciţii:
1.Pokazat că aceste funcții sunt soluții ale ecuațiilor integrale respective.