Pentru a determina o statistică așteptare M * și D * variație statistică a variabilei aleatoare X. construi o histogramă a populației statistice.
Decizie. Într-o distribuție continuă a gamei caracteristică întreg în care sunt închise toate valorile observate trăsătură este împărțită într-un număr de intervale parțiale de lungime h și a găsit mi - variante de frecvență sumă care aparține unei i-lea interval. frecvențele histogramei se numește o formă în trepte constând din dreptunghiuri ale căror baze sunt intervale de lungime h. și o înălțime egală cu raportul mi / h (densitatea de frecvență).
Zona histograma frecvențelor egală cu suma tuturor frecvențelor, și anume, volumul eșantionului. Încercarea de histogramă de frecvență prezentat în Fig. 14.
Estimările nepărtinitoare M * și D * sunt găsi, intervale de a lua mijlocul ca opțiuni:
M * = (-450) · 0,01 + (-350) · + 0,03 (-250) · + 0,07 (-150) · + 0,14 (-50) · 0,25 + 50 · 0,24 +
+ 150 + 250 · 0,15 · 0,08 + 350 · 0,02 + 450 · 0,01 = 0.
Estimarea abaterii standard
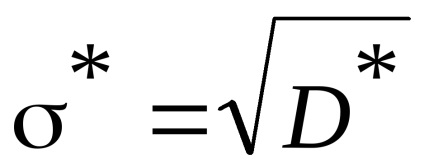
Evaluarea parametrului necunoscut al numărului unic de populația generală se numește o estimare punct.
Împreună cu estimările există estimarea intervalului, atunci când datele eșantionului este construit interval numeric în raport cu care probabilitatea preselectată se poate spune că parametrul estimat este în acest interval. Estimarea Interval este deosebit de necesar pentru un număr mic de observații, în cazul în care punctul de estimare este în mare măsură întâmplătoare, prin urmare, puțin fiabile.
6.7. Găsiți încredere estimări interval de încredere cu probabilitatea necunoscută o așteptare 0,95 caracteristică populația generală X distribuită în mod normal, în cazul dat o deviație standard generală σ = 5, proba medie a * = 14 volum și n = 25 de probă.
Decizie. Pentru a determina acuratețea estimării unui * în statistica matematică sunt intervalele de încredere și pentru a determina fiabilitatea - probabilitatea de încredere. Intervalul de apel Trust, care este o fiabilitate β predeterminată acoperă parametrul estimat.
Densitatea de probabilitate a unei variabile aleatoare normal distribuită este de forma:
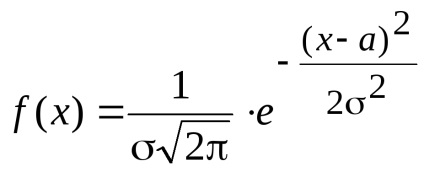
în cazul în care - deviația standard, și - așteptări.
Pentru a estima așteptarea unei variabile aleatoare X distribuite în mod normal, în medie, un eșantion * cu un cunoscut σ deviație standard a populației totale servește interval de încredere
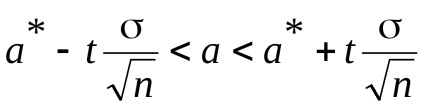
unde
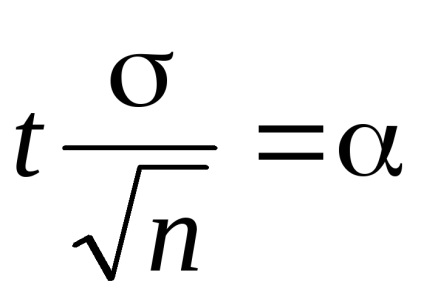
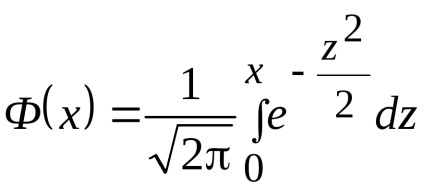
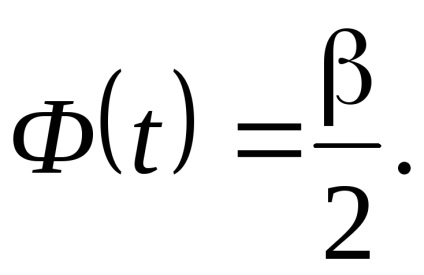
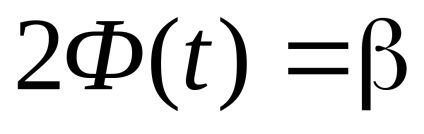
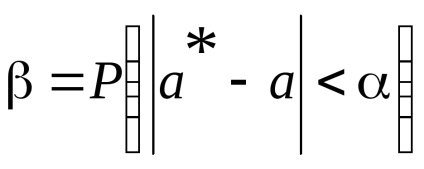
Am găsit un interval de încredere (a * - α, un * + α). Pentru aceasta vom găsi t. din relația