Substituind în ecuația (1.63) valorile b0 = ia0 0 = a2 = 0. Obținem o ecuație stare de următoarea formă (ecuații diferențiale de ordinul întâi):
Nivel de ieșire parametru proporțional cu integrala parametrul de intrare și este descrisă de următoarea expresie:

Funcția de transfer de integrare link-ul trebuie să fie găsite folosind transformata Laplace va avea forma:

În acest caz, k - coeficientul de legătură de transmisie, dimensiunea care este determinată de raportul dimensiune a ratei de schimbare a parametrului de ieșire la dimensiunea de intrare.
Funcția de legare tranziție cu x (t) = 1 (t) are următoarea reprezentare:

În acest caz, C - o constantă de integrare, cu condițiile inițiale egale cu zero.
La un parametru constant de intrare feedback-parametru de ieșire poate fi variată, după cum constantă de integrare poate avea valori diferite în legătură cu unitatea de integrare numit astatic. În cazul în care valoarea parametrului de intrare
se reduce la zero, în contrast cu câștigul proporțional, în integrarea valorii parametrului link-ul de ieșire nu va tinde la zero.
Integratorul de asemenea, numit integrator. Pentru integrator APFC substituit în expresia (. 1,70) Jw în loc de p, și obținem:

Din expresia arată că frecvența reală Re caracteristică (w) este egal cu zero, caracteristica de frecvență imaginară coincide cu răspunsul de frecvență:

În continuare, vom găsi integrator PFC după cum urmează:

Din aceasta rezultă că integratorul atenueaza frecvențe înalte și rapeluri nelimitat frecvențe joase. Amplitudinea de nulyus de ieșire forma de undă tinde să crească frecvența vibrațiilor de intrare, în timp ce trecerea de faza este constantă și este egală cu - π / 2.
Caracteristicile de nivel Reprezentarea grafică arată în figura 30.
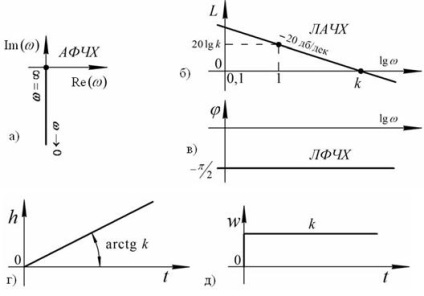
Fig.30. Caracteristici care integrează componenta a), b), c) - frecvența;
Existent reală integrarea unităților characterized''nakaplivaniem „“ acțiune de intrare și posedă apreciabilă yn ?? ertsionnostyu.
Integratorul nu poate fi în echilibru la orice valoare constantă a semnalului de intrare.
Sub influența orice valoare minimă a parametrului de intrare, o ieșire neĸᴏᴛᴏᴩᴏᴇ valoare a parametrului în timp poate deveni
disproporționat de mare. Poziția de echilibru în link-ul se realizează numai atunci când nici o acțiune de intrare.
Exemple de unități existente ale condensatorului pot servi drept (capacitate electrică), un amortizor hidraulic, etc. Conducerea Integrator idee reală prezentată în figura 31.

Fig.31. Reprezentarea efectivă a integrator (condensator)
a se vedea, de asemenea,
Integratorul - o unitate a cărei ieșire este proporțională cu timpul integrală a maretiei de intrare. 1.53 1.54 unde k - factorul de proporționalitate dat link-ul. Rata de integrator de ieșire măreție schimbare, proporțională cu intrare. [Citește mai mult].
Funcția de transfer: W (p) = k / p. Să considerăm cazul special în care k = 1, adică W (p) = 1 / p. APFC: W (j . [Citește mai mult].
Legătură ecuație diferențială este de obicei scrisă în formularul de mai jos. (3.44) unde k1 - cantitatea dimensionale ca în (3.36). Dacă hvyh (t) și x € X (t) au aceeași dimensiune, dimensiunea k1 este de 1 / p. Apoi, (3.44) pot fi reprezentate. (3.45), în cazul în care; - constante de timp. [Citește mai mult].
Dinamica procesului într-o unitate de următoarea ecuație. unde k - câștig. 1. Tranzitorii de răspuns: 2. Răspunsul la impuls: 3. Funcția de transfer a unui integrator real: link-ul de integrare reală. [Citește mai mult].
Legătură ecuație diferențială este de obicei scrisă în formularul de mai jos. (3.44) unde k1 - cantitatea dimensionale ca în (3.36). Dacă hvyh (t) și x € X (t) au aceeași dimensiune, dimensiunea k1 este de 1 / p. Apoi, (3.44) pot fi reprezentate. (3.45), în cazul în care; - constante de timp. [Citește mai mult].
Dinamica procesului într-o unitate de următoarea ecuație. unde k - câștig. 1. Tranzitorii de răspuns: 2. Răspunsul la impuls: 3. Funcția de transfer a unui integrator real: link-ul de integrare reală. [Citește mai mult].
Construcția este realizată conform formulei. Cu valorile date ale k și T. Prin setarea w = 0; 10; 20; 30; 50; . [Citește mai mult].
Construcția este realizată conform formulei. Cu valorile date ale k și T. Prin setarea w = 0; 10; 20; 30; 50; . [Citește mai mult].
Alte nume inerțial element de - elementul aperiodice al primului ordin. Descris de ecuația diferențială (3.3) unde T - nivelul constant de timp, k - câștig. Ecuația operatorului (Tp + 1) Y (p) = kx (p). Atunci când funcția de transfer p = 0. [citeste mai mult].
Alte nume inerțial element de - elementul aperiodice al primului ordin. Descris de ecuația diferențială (3.3) unde T - nivelul constant de timp, k - câștig. Ecuația operatorului (Tp + 1) Y (p) = kx (p). Atunci când funcția de transfer p = 0. [citeste mai mult].