Trasarea funcții
La sfârșitul secțiunii practice a acestui capitol am decis să adăugați un alt paragraf care descrie o metodă de grafice tuturor funcțiilor din sistemul KOMPAS-Graphic. Această problemă a fost ridicată în mod repetat de către utilizatori în timp ce lucrează cu programul, și multe dintre ele nici nu sunt conștienți de posibilitatea inerentă KOMPAS-grafic de construire a funcțiilor din ecuațiile lor.
Mai ales în acest scop, sistemul are o anexă separată - FTDraw bibliotecă, pe care o puteți găsi în alte biblioteci Manager. Biblioteca vă permite să efectuați următoarele acțiuni (a se vedea figura 2.144.):
• construirea graficelor de dependențe funcționale în coordonate carteziene;
• funcții complot în coordonate polare;

Fig. 2.144. bibliotecă FTDraw
După ce a început managerul bibliotecii se deschide meniul său format din două comenzi: diagrame bibliotecă FTDraw și calculator matematice simple. Noi, desigur, sunt mai interesați în prima echipă. După dublu-clic pe ea se va deschide fereastra principală a bibliotecii (vezi. Fig. 2.144), în cazul în care puteți decide modul în care trasarea.
Înainte de a începe biblioteca este necesară pentru a crea (sau a face activ) desen sau fragment.
Să ne uităm la un exemplu de reprezentarea grafică a unei funcții complexe în coordonate carteziene. Să presupunem că funcția considerată a forma y (x) = 4? X + 3cos (x) + 2ln (x) în intervalul de la 0,1 la 100. Click pe primul din fereastra bibliotecii principale mari butoane pătrate pentru a merge la modul diagrame în coordonate carteziene. Ca urmare, o fereastră nouă (Fig. 2.145) se deschide în fața ta, în care specificați ecuația prin care va fi construit programul, precum și opțiuni implicite.
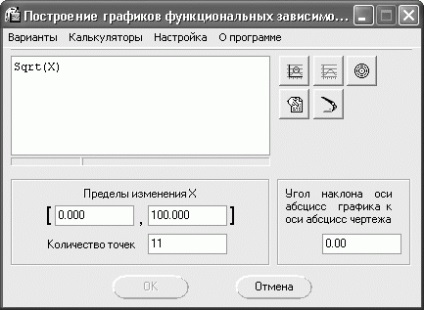
Fig. 2.145. Trasarea funcții în coordonate carteziene
Implicit, caseta este sqrt (x) pentru introducerea funcției, ceea ce înseamnă că sistemul este configurat pentru complot y (x) =? X. Acest utilitar are o sintaxă foarte simplă, în afară, aveți posibilitatea să utilizați întotdeauna un indiciu la selectarea funcției dorite, faceți clic dreapta în câmpul în care doriți să introduceți formula (Fig. 2.146).
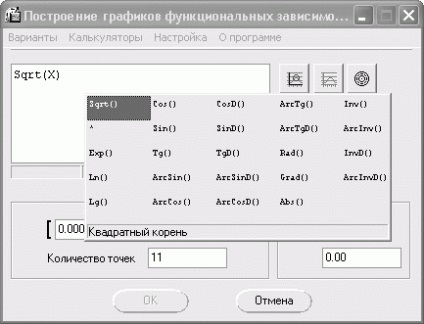
Fig. 2.146. Sfat pentru selectarea și introducerea funcțiilor
Folosind sfaturile de mai sus și tastatură, introduceți în următoarele funcții linia 4 * sqrt (x) + 3 * Cos (x) + 2 * Ln (x). Apoi setați intervalul dorit în domeniul limitelor X schimba, și în numărul de puncte setat la 50. Faceți clic pe Specificați poziția punctului de bază a graficului
apoi faceți clic pe la punctul în care doriți să plasați grafica de origine generată. După punctul de setare, sistemul revine la fereastra sarcinii dependențe funcționale, care trebuie acum să fie activat butonul Plot
Faceți clic pe acest buton, apoi apăsați pe OK, pentru a finaliza construcția. Dacă ai făcut totul bine, rezultatul ar trebui sa graficul prezentat în Fig. 2.147.

Fig. 2.147. Diagrama funcției în coordonate carteziene
Ca un alt exemplu, aici ordinea reprezentarea grafică în coordonate polare. Pentru a realiza o examinare simplă și suficient de cunoscută spirală Arhimede, ecuația care, în coordonate polare este dată de r = k j, unde k - coeficient arbitrar altul decât 0.
Porniți din nou biblioteca FTDraw și apăsați butonul de pe al doilea modul de funcționare mare drept reprezentarea grafică în coordonate polare. Linia egală cu 200 (Fig. 2.148) pentru a introduce formule X * 2, setați intervalul de la 0 la 20 * Pi, precum și numărul de puncte.
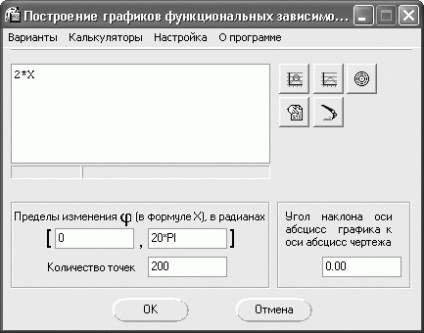
Fig. 2.148. Trasarea funcții în coordonate polare
După ce specificați punctul de plecare pentru construirea, faceți clic pe butonul devine Plot și OK. Ca rezultat, veți obține o spirală Arhimede, pe baza unui pasaj din sistem KOMPAS-3D (Fig. 2.149).
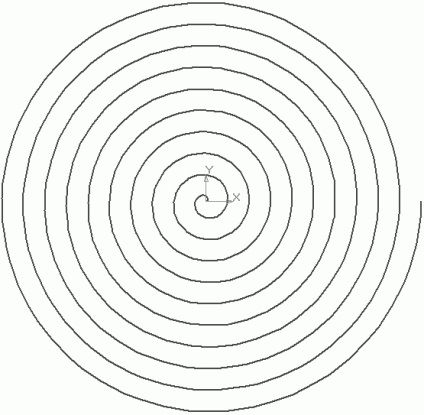
Fig. 2.149. spirală Arhimede
Ponderea pe pagina