Rezolvarea inegalităților pătratice. metodă grafică
Rezolvarea inegalităților pătratice.
Piața va fi numit inegalitatea de forma:
sau.
Notă: semnul inegalității poate fi orice indiciu de bază că inegalitatea pătratice este că, în comparație cu zero, de gradul doi polinomiale.
Acest articol va fi discutat mai multe metode de rezolvare a inegalităților pătratice și arată relația dintre aceste metode.
Metoda I .ca grafic principal.
Exemplul 1: rezolva inegalitatea. Pe partea stângă este trinomul pătratic. Construi programul său, adică grafic al funcției. Toată lumea știe că graficul unei funcții pătratică este o parabolă.
Notă: Algoritmul de construcție schematică a unei parabole:
1) Se determină direcția ramurilor.
În cazul în care ramura îndreptată în sus, dacă și în jos.
În cazul - ramurile sunt îndreptate în sus.
2) Se determină coordonatele intersecției graficului de axa x. Ordonatele acestor puncte sunt 0, adică, în funcție este necesară pentru a înlocui și de a rezolva ecuația rezultată.
În cazul în care:
Astfel, graficul funcției intersectează axa x la punctele cu coordonatele.
Notă: Dacă o ecuație pătratică nu are rădăcini, parabolei traversează axa x nu este.
3) element opțional dacă parabolei intersectează axa absciselor a graficului.
Se determină coordonatele vârful parabolei.
În cazul în care:
coordonatele vertex.
Noi construim o parabole, pe baza faptelor obținute:
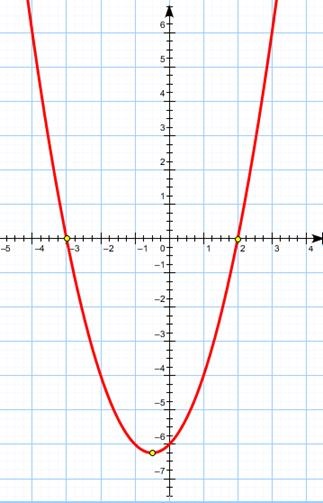
Să ne amintim că problema este rezolvată
inegalitatea inițială poate fi scrisă ca: în cazul în care.
Decizia se va abscisă (coordonatele) ale punctelor graficului, ordonata (coordonate) este mai mare decât zero, adică, se află în jumătatea superioară. Să ne explicăm această afirmație printr-un exemplu.
EXEMPLU (un caz special):
Să considerăm un punct A (vezi. Fig.) Coordonatei.
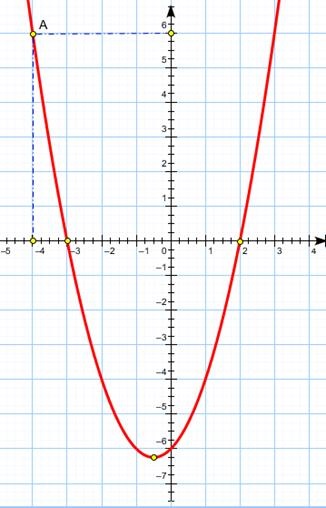
Acesta se află în partea superioară semiplanul, adică, abscisa său este soluția inegalității.
Citește:
a) Din punct de vedere algebric:
Substituenților în inegalitate:
Inegalitatea este adevărat, atunci o soluție a inegalității.
b) Din punct de vedere geometric. Amintiți-vă că a construit o parabolă și este considerat punctul A cu abscisa. Calculăm ordonata. . Ordonata a acestui punct este pozitiv faptul că ochiul liber se poate vedea pe grafic. și anume inegalitate este îndeplinită.
Trebuie remarcat în albastru, în parcelele figura grafic, pentru care următoarea condiție:
Scriem abscisa punctelor (piesele necesare Abscisa notate cu eclozare). Acesta va fi răspunsul la inegalitate.
răspundă:
EXEMPLUL 2:
Rezolva inegalitatea.
Am construit parabolei schematică
1) ramurile de direcție.
, ramură parabole îndreptate în sus.
2) intersecția cu OX.

Parabolei intersectează axa abscisei la punctele cu coordonatele.
3) coordonatele nodurilor:
Coordonatele vârful parabolei:
Noi construim grafic:
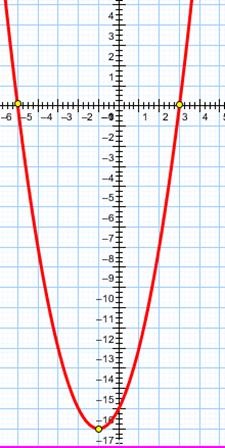
Inegalitatea poate fi scris ca în cazul în care. Ie soluții pentru puncte interesante de inegalitate, ordonata din care este mai mică sau egală cu zero, adică puncte care se află în jumătatea inferioară sau OX.
Notă aceste puncte:
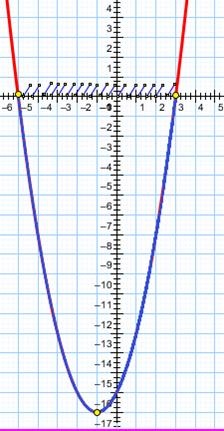
Eclozarea denota abscise acestor puncte și scrie un set de :. Aceste valori sunt variabile și vor fi soluția inegalității.
răspundă:
EXEMPLUL 3:
Rezolva inegalitatea.
Am construit parabolei schematică
1) ramurile de direcție.
, ramură parabole îndreptate în sus.
2) intersecția cu OX.
Nu există rădăcini.
Parabole intersectează axa x.
3) a nodului coordonatele:
Coordonatele vârful parabolei:
Noi construim grafic:
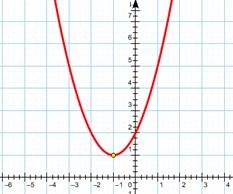
Inegalitatea poate fi scris ca în cazul în care. Ie soluții pentru puncte interesante de inegalitate, ordonata din care este mai mică sau egală cu zero, adică Punctele situate în jumătatea inferioară sau axa x. Nu există astfel de puncte, astfel cum toate parabolei este deasupra axa x. Efectuarea de ieșire corespunzătoare.
Raspuns: nu există soluții, adică nu există nici o astfel de valori variabile la care inegalitatea - dreapta.