Câmpul magnetic al curenților de direcți ai diferitelor configurații studiate experimental de savantul francez Zhan Batist Biot și Feliksom Savarom (1820). Ei au ajuns la concluzia că curenții de inducție magnetică care circulă prin conductorul este determinat prin acțiunea combinată a tuturor porțiunilor conductoare individuale. Câmpul magnetic este supus principiului superpoziției:
În cazul în care câmpul magnetic este generat de conductoare multifilare cu curent, inducția câmpului rezultant este suma vectorială a câmpurilor de inducție produse de fiecare conductor individual.
conductor de curent cu inducție poate fi reprezentat ca o suma vectorială a inductiile elementare produse de porțiuni individuale ale conductorului. Experimental, este imposibil să se aloce o parte separată a conductorului cu curent, deoarece curenții constante sunt întotdeauna închise. Putem masura doar inducția magnetică totală creată de către toate elementele curente. legea Biot-Savart definește contribuția la inducția magnetică a câmpului magnetic rezultat produs de o mică porțiune δl conductor cu I. curent
Aici, r - distanța de la această porțiune δl la punctul de observație, α - unghiul dintre direcția punctului de observație și direcția curentului la această porțiune, μ0 - permeabilitatea vid. direcția vectorului determinat de o regulă de degetul mare: coincide cu direcția de rotație a mânerului cu degetul mare mișcarea de translație de-a lungul curentului. Fig. 1.17.1 ilustrează legea Biot-Savart de exemplu rectiliniu conductor de câmp magnetic. Dacă suma (integra), contribuțiile la câmpul magnetic al tuturor secțiunilor individuale ale conductorului liniar cu un curent, formula se obține pentru un câmp magnetic de inducție de curent continuu:
care a dus deja la 1.16.
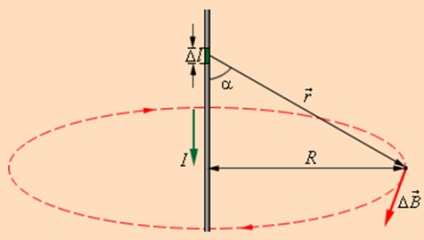
Ilustrarea legii Biot-Savart
legea Biot-Savart pentru a calcula câmpul magnetic permite curenți de diferite configurații. Este ușor, de exemplu, efectuați un calcul al unui câmp magnetic în centrul unei bobine circulare, cu un curent. Acest calcul conduce la formula
unde R - raza unui conductor circular. Pentru a determina direcția vectorului este de asemenea posibil să se utilizeze regula din dreapta, doar acum este necesar să se rotească mânerul în direcția circulară mișcării curente și de translație a degetului mare va indica direcția vectorului de inducție magnetică.
Calculele câmpului magnetic este adesea mai simplu atunci când înregistrat simetrie în configurația actuală, producând câmpul. În acest caz, este posibil să se utilizeze teorema de circulație a inducției magnetice. în care curentul magnetic teoria câmpului joacă același rol ca și teorema lui Gauss în electrostatica.
Clarificarea conceptului de circulant vector Let în spațiu în care se creează câmpul magnetic, selectat unele circuit închis convențional (nu neapărat plană) și indică direcția pozitivă a traversal. În fiecare zonă mică δl acest circuit poate determina componenta tangențială a vectorului la acea locație, adică pentru a determina proiecția vectorului pe direcția tangentei la această porțiune a circuitului (Fig. 1.17.2).
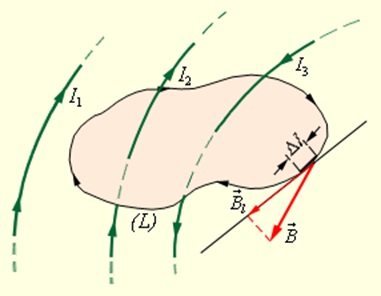
buclă închisă (L) pentru a specifica direcția traversal. Acesta arată curentul I1. I2 și I3. crearea unui câmp magnetic
bucla vector se numește suma produselor δl. luate în jurul conturului L:
Unii Curenții creează un câmp magnetic poate pătrunde în circuitul L selectat în timp ce celelalte curenții pot fi în partea laterală a conturului.
Teorema Circulation afirmă că circulația câmpului magnetic circuitul de curent constant în conformitate cu oricare L este întotdeauna egală cu produsul dintre constanta magnetic μ0 suma tuturor curentilor penetrante circuitului:
Ca un exemplu, în Fig. 1.17.2 prezintă mai mulți conductori cu curenți de a crea un câmp magnetic. Curenții I2 și I3 permeat buclă L în direcții opuse, acestea trebuie să fie atribuite semne diferite - considerate pozitive curenți, care sunt asociate cu regula șurub buclă direcția parcurgeri dreapta selectată (degetul mare). În consecință, I3> 0 și I2 <0. Ток I1 не пронизывает контур L .
Teorema Circulation în exemplul de față este exprimat prin relația:
Teorema privind circulația rezultă în general din legea Biot-Savart și principiul superpoziției.
Cel mai simplu exemplu de utilizare a teoremei de circulație este o derivație pentru conductorul rectiliniu inducție câmp magnetic. Având în vedere simetria unei anumite sarcini, circuitul L este recomandabil să se aleagă o circumferință de o anumită rază R. situată într-un plan perpendicular pe conductor. Centrul cercului este la un anumit punct al conductorului. Prin vector simetrie este direcționată tangențial, iar unitatea sa este aceeași în toate punctele de circumferință. Utilizarea teoremei de circulație conduce la relația:
unde formula pentru magnetic de inducție câmp conductor modulului liniar cu un curent dat anterior.
Acest exemplu arată că circulația magnetic de inducție vector teorema poate fi utilizat pentru calcularea câmpurile magnetice produse de curenții de distribuție simetrică în cazul în care din considerente de simetrie poate „ghici“ structura globală a câmpului.
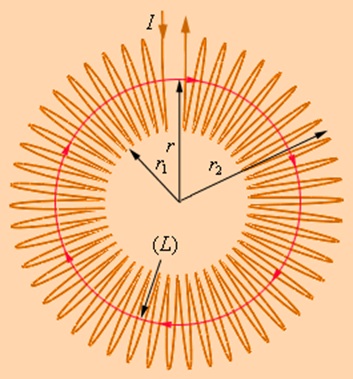
Există o mulțime de exemple practice importante de calcul al câmpurilor magnetice cu ajutorul teoremei de circulație. Un astfel de exemplu este problema calculului câmpului bobinei toroidale (Fig. 1.17.3).