Definim proprietățile relației.
1) reflectorizant. deoarece . Graficele reflexive reflectă prezența buclei la fiecare nod.
2) Nu antireflexive. deoarece existența reflexivității - a negat anti-reflexie.
3) Nu simetric. deoarece în prezența perechii (1, 2) nu există nicio pereche (2, 1) și mijloace este încălcat regula (în coloana nici nervuri simetrice).
4) Nu antisimetrică. deoarece este reflexiv, prix atunci regula este încălcată = y.
6) tranzitivitate. deoarece dacă «x y divizorul» și «y divizor z», «x» z divizorul. Coloana toate lanțurile construite de la x la y - margine închisă (x, y).
De exemplu: (1, 3), (3, 6) (1, 6)
(1, 2), (2, 2) (1, 2), etc.
7) Nu finaliza. deoarece nu despre orice pereche de x și y poate fi spus sau. De exemplu: (2, 5) R și (5, 2) R. Aceste noduri sunt conectate de margini.
Astfel, raportul dintre reflectorizantă identic tranzitiv. înseamnă o relație de ordine.
2) găsi pentru a construi un grafic:
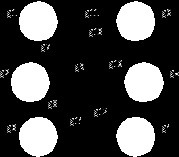
d) raza, diametru, centrul, nodurile periferice;
Centrul este un vârf al graficului, care realizează cea mai mică dintre abaterea. Centrele pot fi multiple, deoarece Abaterea numai la vârful 1, deci este - Center.
Count Deviația raza se numește centrul p (G) = d (1) = 1.
Diametrul graf neorientat este cea mai mare distanta dintre nodurile. Și distanța - este lungimea celui mai mic circuitul elementar. Diametrul Fgrafa poate fi numit
2) lungimea maximă a unui mod elementar, atunci D (G) = 1.
nod periferic este un vârf cu cea mai mare deviație. Acesta este un 2, 3, 4, 5, 6.
e) Numărul stabilității interne și externe.
Grafic intern set stabil G (x) - S este un subset al setului de vârfuri X. oricare două vârfuri care nu sunt adiacente. Numărul α rezistenței interne (G) - puterea maximă la interior set stabil.
, ,
set stabil de la exterior graficului G (x) - T este un subset din multitudinea de noduri fiecare X. vertex acela al X \ T = arc conectat la vârful T.
Numărul de β de stabilitate externă (G) - minim de putere set extern stabil. .
3) Pentru cele două grafice selectate aleatoriu și găsi suma cartezian produsului cartezian.
a) o multitudine de vârfuri X este produsul cartezian al seturilor X1 și X2. și anume X1 × X2 =.
b) o multitudine de vârfuri adiacente vertex (x1, x2) a unui produs cartezian a două grafice este definit ca produsul cartezian al seturilor de noduri ale G1 grafic (X1), x1 adiacent și graficul G2 (X2) adiacent x2.
1) definește setul de noduri ale G (X) și se construiește un grafic:
Vârfurile adiacente unei.
Nodurile adiacente x. , TogdaG (a, x) =.