Matrix algebra - matrice inversă
Matricea Inversul este o matrice care, atunci când este multiplicată, ambele dreapta și stânga pe această matrice dă matricea de identitate.
Matricea inversă denote A la matrice prin, apoi în conformitate cu definiția obține
unde E - matricea identitate.
Matricea pătrat se numește nesingular (nedegenerat) dacă este determinant său este nenul. În caz contrar, se numește specială (degenerat) sau singular.
Următoarea teoremă are: fiecare matrice non-singulară are o matrice inversă.
Operația de a găsi matricea inversă se numește inversiune matrice. Luați în considerare algoritmul de inversare matrice. Să o matrice nesingular de ordinul n:

unde Δ = det A ≠ 0.
Elementamatritsy cofactor n ordine A este luat -lea cu un anumit semn al determinantul (n-1) ordine obținută prin ștergerea -lea coloana i -lea -lea rând și j al matricei A.

Forma matricea Adjoint așa-numitele:

cofactori undeva corespunzătoare A. elementovmatritsy
Rețineți că cofactori a elementelor din rândurile matricei A sunt aranjate în coloanele respective ale unei matrice. care este, în același timp, a produs o matrice transpusa.
Împărțind toate elementele unei matrice pe Δ - valoarea determinantul matricei A se obține ca rezultat al matricei inverse:
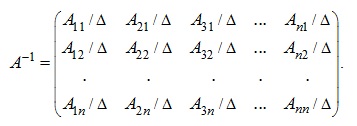
Notă unele proprietăți speciale ale matricei inverse:
1) pentru o matrice dată A este doar matricea inversă;
2) dacă există o matrice inversă, dreapta și stânga inversa matricea inversă coincide cu ea;
3) speciale (degenerat) matrice pătrată nu are o matrice inversă.
Principalele proprietăți ale matricei inverse:
1) determinantul matricei inverse și determinantul matricei inițiale sunt de reciproce;
2) inverse produs matrice pătratică de matrici este factori proizvedeniyuobratnyh, luate în ordine inversă:
3) transpusa matricei inverse este egală cu matricea inversă prin transpoziția matricei:
EXEMPLU EXEMPLU. Calculati inversul acestei:
. R e w n e determinant al matricei A este egal cu:
Prin urmare, matricea A este nesingular. Adjoint à matrice este:
Împărțind toate elementele conectate la matricea Δ = 1, obținem matricea inversă:
Verificăm că, într-adevăr,
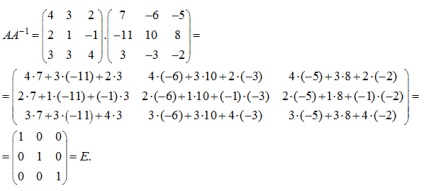
Astfel, matricea inversă este găsită o matrice dată A.