Comparând aceste ecuații arată că derivatul la un anumit punct de pe vectorul traseu are o valoare maximă atunci când direcția vectorului coincide cu direcția gradientului. Aceasta este cea mai mare valoare a derivatului egal cu modulul gradientului în acest punct. Prin urmare, vectorul gradientului indică direcția cea mai mare creștere a funcției, la acel moment, iar unitatea sa - rata maximă de creștere.
Exemplul 16.8. Funcția Dana. Găsiți derivatul la punctul
M (1, 1, 1), în direcția vectorului gradientului și vectorul. Comparați rata funcției schimbare în aceste zone.
Decizie. În scopul de a găsi derivatul în direcția vectorului, mai întâi găsi magnitudine și direcție cosinus sale.
Noi găsim derivatele parțiale ale funcției de la punctul:
Funcțiile derivate ale direcției vectorului:
Noi construim gradientul vector al derivatelor parțiale găsit la punctul M și găsiți modulul său:
care este de așteptat să fie.
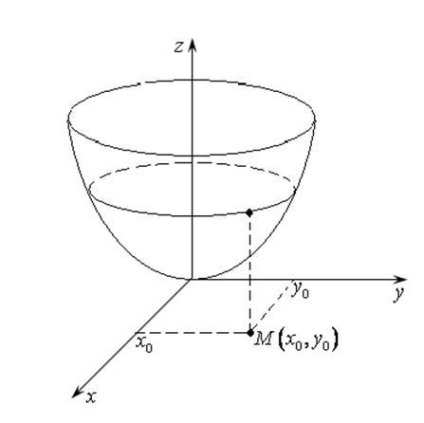
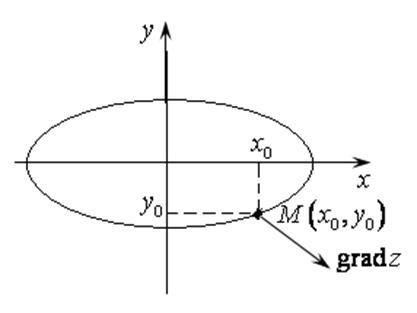
Dacă funcția este o funcție de două variabile, vectorul
la punctul se află în planul HOY și perpendicular pe suprafața secțiunii de proiecție Hoy plan paralel. (Fig. 16.5).
16.7. concluzie
Noi tragem primele concluzii pe această temă.
1. Schimbare U Legea una variabilă în funcție de două sau mai multe variabile x reciproc independente. în etc. Se numește o funcție de mai multe variabile.
2. Modificările U asupra diferitelor variabile diferă unul de altul și sunt caracterizate prin derivate parțiale. derivate parțiale arată rata de schimbare în direcția sa.
3. Rata de schimbare într-o direcție arbitrară caracterizată vectorul ponapravleniyu derivat.
4. Direcția în care viteza este mai mare, dată de vectorul având un gradient de un nume special. Coordonatele sale sunt egale cu valoarea derivatelor parțiale la acest punct și modulul - rata de schimbare.
Curs 17.
derivați de ordin superior.
Funcția EKSTEMUM a două variabile
9. derivatele parțiale ale ordinelor superioare.
10. Extrema funcțiilor de două variabile.
11. Cea mai mare și cea mai mică valoare a unei funcții în zona închisă.
12. Parametri de selecție pentru formulele empirice mai simplă formă prin metoda celor mai mici pătrate
17.1. introducere
In studiul funcțiilor unei variabile, în plus față de derivatul de prim ordin, care caracterizează viteza de schimbare a unui proces, am introdus conceptul de derivata a doua, care a fost responsabil pentru accelerație. La o funcție de două variabile, există două derivate parțiale, care, în general, sunt de asemenea funcții ale aceleași variabile, și, prin urmare, din nou, ele pot diferenția și x. și y. Vom arăta cum se face.
17.2. derivați de ordin superior
Lăsați funcția z = f (x, y) este continuă cu derivații lor parțială și într-o anumită regiune D HOY plane.
Determinarea 17.1.Chastnymi de ordinul doi (sau al doilea derivatele parțiale) sunt derivații menționați și derivați.
Al doilea derivatele parțiale sunt indicate după cum urmează:
Aici funcționează secvențial diferențiate în raport cu x de două ori;
aici f este diferențiată în raport cu x mai întâi. și apoi rezultatul y;
aici f este diferențiată de la prima supra. și apoi rezultatul x;
aici f este diferențiată de două ori în raport cu y.
Primul și ultimul derivatele sunt numite uneori pur. iar al doilea și al treilea - derivatele mixte de ordinul doi.
Acesta poate fi dovedit (a se vedea. Kramer tutorial)) care
cu condiția de continuitate a derivaților la punctele prestabilite, adică. e. al doilea derivat mixt nu depinde de ordinea de diferențiere și, prin urmare, patru derivate parțiale sunt reduse la trei.
derivați de a doua poate fi din nou diferențiate atât în x. și în y. Obținem derivați treilea ordin, dintre care două sunt curate, iar celelalte șase - mixte:
Aici vom lua în considerare faptul că
și, prin urmare, opt parțial redus la patru.
Acest proces poate continua să primească și derivații de orice ordine, cu condiția ca acestea să fie continuă la un punct predeterminat.
Exemplul 17.1. Calculați instrumentele derivate de ordinul doi ale funcției
Decizie. Găsim derivații de prim ordin, având în vedere faptul că derivata parțială în raport cu x este calculată în ipoteza că - constantă și vice-versa:
Noi găsim derivații de ordinul doi
Exemplul 17.2. Funcția Dana. Arătați că.
Decizie. Găsim succesiv valorile tuturor instrumentelor derivate și să verifice această egalitate.
Înlocuim valorile găsite în ecuația originală:
Vedem că ecuația pentru funcția specificată este executată.
Exemplul 17.3. Funcția Dana. Arătați că.
- o parte din stânga.
Pentru a calcula dreptul să ia în considerare ceea ce este deja cunoscut, și pentru a găsi
astfel egalitatea inițială la funcția specificată.
După cum se poate observa din exemplele de mai sus, ar trebui să fie vigilenți și să se separe, în măsura în care este posibil acele variabile, care, în acest caz, acționează ca o constantă.
17.3. Extremele funcțiilor de două variabile
Am discutat despre extremele funcțiilor de o variabilă în detaliu. Noi transfera aceste cunoștințe pentru funcția de două variabile.
Definiția 17.2. Punctul se numește o funcție maximă dacă
pentru toate punctele (x, y) este suficient de aproape de punctul și distinct de acesta (Fig. 17.1).
Definiția 17.2. Un punct se numește punctul de minim al funcției, în cazul în care
pentru toate punctele (x, y) este suficient de aproape de punctul și distinct din acesta. (Fig. 17.2).
Punctele în care derivatele parțiale egale cu zero sau nu există, numite critice.
Uneori, punctul de extremelor, și este posibil să se determine natura bunului simț.
De exemplu, funcția are un minim la u, adică punctul M (1,2). Intr-adevar, pentru orice primul termen va continua să crească, și - de asemenea, prin urmare, la punctul M (1.2) are cel mai puțin, cu (figura 17.1.).
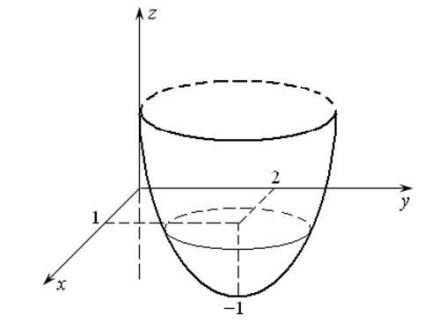
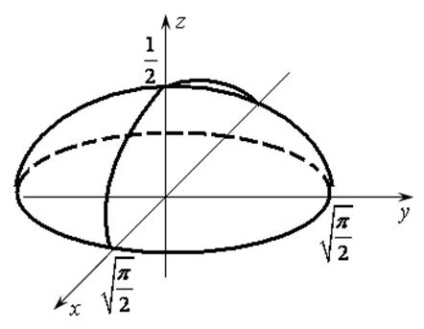
Funcția are un maxim la punctul (0,0) și (Fig. 17.2).