Să începem cu câteva definiții. Polinom de gradul n-lea (sau n-th-order) va fi numită o expresie de forma $ P_n (x) = \ sum \ limits_ ^ a_x ^ = a_x ^ + a_x ^ + a_x ^ + \ ldots + a_x + a_n $. De exemplu, expresia $ 4x ^ + 87x ^ 2 + 4x-11 $ este un polinom al cărui grad este $ 14 $. Acesta poate fi descrisă după cum urmează: $ P_ (x) = 4x ^ + 87x ^ 2 +-4x 11 $.
$ $ A_0 factor numit lider coeficientul de polinomului $ $ P_n (x). De exemplu, pentru polinomul $ 4x ^ + 87x ^ 2 + 4x-11 $ coeficientul de conducere este egal cu $ 4 $ (număr înainte de a $ x ^ $). Numărul de $ a_n $ este numit termenul constant al polinomului $ $ P_n (x). De exemplu, pentru un $ 4x ^ + 87x ^ 2 + 4x-11 $ $ termen constant egală cu (- 11) $. Acum, să ne întoarcem la teorema, care, strict vorbind, și materialul de prezentare se va baza pe aceasta pagina.
Pentru oricare două polinoame $ P_n (x) $ si $ G_m (x) $ pot fi găsite astfel de polinoame $ Q_p (x) $ si $ R_k (x) $, care de capital vor fi efectuate
Expresia "divide un polinom $ P_n (x) $ în polinom $ G_m (x) $" înseamnă "pentru a prezenta un polinom $ P_n (x) $ sub forma (1)." Să ne numim un polinom $ P_n (x) $ - divizibile polinom $ G_m (x) $ - împărțitor polinom $ Q_p (x) $ - coeficientul de $ P_n (x) $ pe $ G_m (x) $, iar $ polinomului R_k (x) $ - ostachey prin divizarea $ P_n (x) $ la $ G_m (x) $. De exemplu, pentru P_6 polinom $ (x) = 12x ^ 6 + 3x ^ 5 + 16x ^ 4 + 6x ^ 3 + 8x ^ 2 + 2x + 1 $ și $ G_4 (x) = 3x ^ 4 + 4x ^ 2 + 2 $ pot fi obținute de o astfel de egalitate:
Aici, $ P_6 polinomul (x) $ este divizibilă cu $ G_4 polinomul (x) $ - divizorul polinom $ Q_2 (x) = 4x ^ 2 + x $ - coeficient de $ P_6 (x) $ la $ G_4 (x) $, iar $ R_3 polinomul (x) = 2x ^ 3 + 1 $ - restul de divizare $ P_6 (x) $ la $ G_4 (x) $. Rețineți că gradul de reziduu (adică, 3) este mai mic decât gradul de divizorul (adică 4), astfel încât ecuația (1) este îndeplinită.
Dacă $ R_k (x) \ echiv 0 $, atunci spunem că polinomul $ P_n (x) $ este împărțit la polinomul $ G_m (x) $ fără urmă. De exemplu, polinomul $ 21x ^ 6 + 6x ^ 5 + 105x ^ 2 + 30x $ divizibil cu polinomul $ 3x ^ 4 + 15 $ nici un reziduu, ca și egalitatea:
Aici, $ P_6 polinomul (x) = 21x ^ 6 + 6x ^ 5 + 105x ^ 2 + 30x $ este divizibil; polinom $ G_4 (x) = 3x ^ 4 + 15 $ - compas; și polinomul $ Q_2 (x) = 7x ^ 2 + 2x $ - coeficient de $ P_6 (x) $ la $ G_4 (x) $. Reziduul este zero.
Pentru a împărți un polinom de o divizie polinom este adesea folosit „coloana“ sau, așa cum este numită „zonă“. Punerea în aplicare a acestei metode Să examinăm exemplele.
Înainte de a merge la exemple, voi introduce un termen mai mult. El nu este universal acceptată. și-l utilizați vom fi numai pentru comoditatea de prezentare. Până la sfârșitul acestei pagini va fi numit un membru senior al polinomului $ P_n (x) expresie $ $ a_x ^ $. De exemplu, pentru $ 4 x ^ polinomul + 87x ^ 2 + 4x-11 $ cel mai mare element este $ 4 x ^ $.
Se împarte $ 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + $ 5 $ 5x ^ 2-x + 2 $, folosind divizia "coloana".
Deci, avem două polinoame, $ P_5 (x) = 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + $ 5 și $ G_2 (x) = 5x ^ 2-x + 2 $. Primul grad egal cu $ 5 $, iar al doilea grad este egal cu $ 2 $. Polinomial $ P_5 (x) $ - dividendul, iar $ G_2 polinomul (x) $ - divizor. Sarcina noastră este de a găsi coeficientul și restul. Sarcina va fi rezolvată pas cu pas. Vom folosi aceeași notație, care este folosit pentru a împărți numerele:
Senior Element divide polinom $ P_5 (x) $ (adică $ 10x ^ $ 5) pe elementul principal al $ Q_2 polinomul (x) $ (adică $ 5x ^ 2 $):
Rezultată expresie $ 2x ^ 3 $ - acesta este primul element particular:
Înmulțiți polinomiale $ 5x ^ 2x + 2 $ la $ 2x ^ 3 $, în timp ce primește:
Scriem rezultatul:
Acum scade din polinom $ 10x ^ 5 + 3x ^ 4-12x ^ 3 + 25x ^ 2-2x + 5 $ polinoame $ 10x ^ 5-2x ^ 4 + 4x ^ 3 $:
Completați acest polinom este deja sub linia:
În această primă etapă se termină. Rezultatul pe care le-am obținut, pot fi scrise într-o formă extinsă:
Deoarece gradul de polinomului $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + 5 $ (adică, 4) este mai mare decât gradul de polinomului $ 5x ^ 2-x + 2 $ (adică, 2), procesul ar trebui să continue împărțirea. Să trecem la al doilea pas.
Acum se va lucra cu polinoame $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + $ 5 și $ 5x ^ 2-x + 2 $. La fel ca și în prima etapă, vom împărți membrul senior al primului polinomului (adică $ 5x ^ 4 $) pe elementul principal al doilea polinomului (adică $ 5x ^ 2 $):
Rezultată $ expresie x ^ 2 $ - aceasta este al doilea membru privat. Adăugăm la $ privat x ^ 2 $
Inmultiti polinom $ 5x ^ 2-x + 2 $ pentru $ x ^ 2 $, în timp ce primește:
Scriem rezultatul:
Acum, se scade din polinomul $ 5x ^ 4-16x ^ 3 + 25x ^ 2-2x + 5 $ polinomiale $ 5x ^ 4-x ^ 3 + 2x ^ 2 $:
Completați acest polinom este deja sub linia:
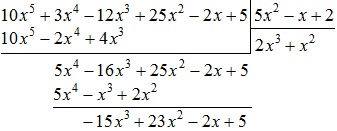
În această a doua etapă se termină. Acest rezultat poate fi scris în formă extinsă:
Deoarece gradul de polinomului $ -15x ^ 3 + 23x ^ 2-2x + 5 $ (adică, 3) este mai mare decât gradul de polinomului $ 5x ^ 2-x + 2 $ (adică, 2), continuând apoi procesul de fisiune. Să trecem la pasul al treilea.
Acum se va lucra cu polinoame $ -15x ^ 3 + 23x ^ 2-2x + $ 5 și $ 5x ^ 2-x + 2 $. La fel ca și în etapele anterioare, împărțiți membrul superior al primului polinomului (adică $ -15x ^ $ 3) de elementul conducător al doilea polinomului (adică 5x $ ^ 2 $):
De $ expresie rezultat (- 3x) $ - aceasta este a treia celulă privată. Completați privat -3x $ $
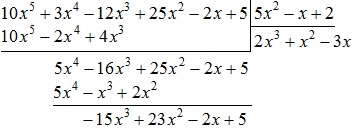
Înmulțiți polinomul $ 5x ^ 2-x + 2 $ la $ (3x) - $, în timp ce a primit:
Scriem rezultatul:
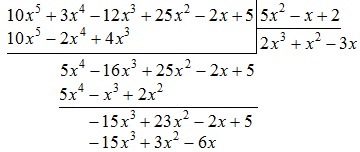
Acum, se scade din polinomul $ -15x ^ 3 + 23x ^ 2-2x + 5 $ polinom $ -15x ^ 3 + 3x ^ 2-6x $:
Completați acest polinom este deja sub linia:
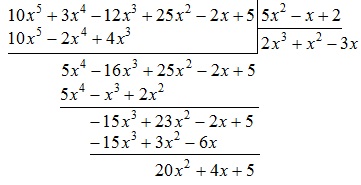
În această a treia etapă se termină. Acest rezultat poate fi scris în formă extinsă:
Deoarece gradul de polinomului $ 20x ^ 2 + 4x + 5 $ (adică 2) egal cu gradul polinomului $ 5x ^ 2-x + 2 $ (adică, 2), continuând apoi procesul de fisiune. Să trecem la a patra etapă.
Acum se va lucra cu polinoame $ 20x ^ 2 + 4x + $ 5 și $ 5x ^ 2-x + 2 $. La fel ca și în etapele anterioare, împărțiți membrul superior al primului polinomului (adică $ 20x ^ 2 $) la un membru senior al doilea polinomului (adică $ 5x ^ 2 $):
Numărul rezultat este de $ 4 $ - acesta este al patrulea element privat. Se umple la privat $ $ 4
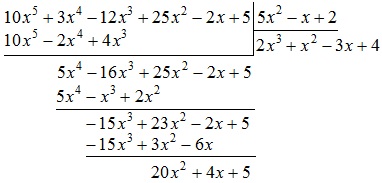
Inmultiti polinom $ 5x ^ 2-x + $ 2 $ 4 $, în timp ce primește:
Scriem rezultatul:
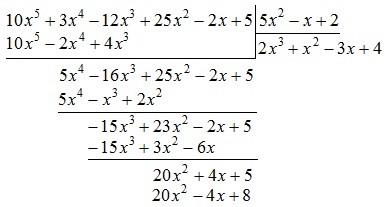
Acum, se scade din polinomul $ 20x ^ 2 + 4x + 5 $ polinom $ 20x ^ 2-4x + $ 8:
Completați acest polinom este deja sub linia:
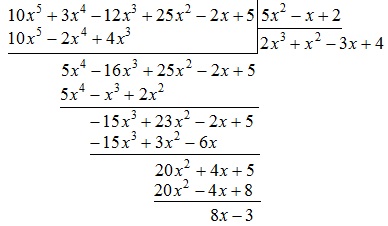
În această a patra etapă se termină. Acest rezultat poate fi scris în formă extinsă:
Deoarece gradul de polinomului $-8x 3 $ (adică, 1) mai mic decât gradul de polinomului $ 5x ^ 2-x + 2 $ (adică, 2), procesul de divizare este finalizat. Coeficientul de $ P_6 polinomul (x) $ de $ G_2 polinomul (x) $ este polinomul $ Q_3 (x) = 2x ^ 3 + x ^ 2-3x + $, 4. Restul de divizare $ P_6 (x) $ la $ G_2 (x) $ - este polinom $ R_1 (x) = 8x-3 $. De fapt, ne-am prezentat inițial polinomul $ P_6 (x) $ sub formă de (1):
Răspuns. prin împărțirea - polinomul $ 2x ^ 3 + x ^ 2-3x + $ 4, restul - polinomul $-8x 3 $.
Se împarte $ 4x ^ 3 + 2x-11 $ la $ x + 5 $, folosind divizia "coloana".
Puteți utiliza schema Horner (și ar fi un pic mai puțin greoaie). Cu toate acestea, în scopuri pur demonstrative folosim diviziunea „coloana“. explicații detaliate sunt în exemplul №1, prin urmare, aici menționăm doar cursul soluției.
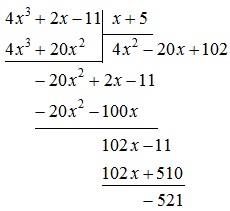
Rezultatul poate fi scris în această formă:
Prin urmare, raportul dintre 4x $ ^ 3 + 2x-11 $ la 5 $ x + $ este polinomul 102 $ 4x ^ 2-20x + $, iar restul este numărul de $ (- 521) $ (de fapt, aceasta este un polinom de ordinul zero ).
Răspuns. Privat - polinom $ 4x ^ 2-20x + $ 102, restul - numărul de $ -521 $.
Divide $ 7x ^ 3 + 9x ^ 2-5x + $ 9 $ 5x ^ 7 + 10x ^ 6-17x ^ 2 +-14x 7 $.
Gradul de divizorul (adică polinom $ 5x ^ 7 + 10x ^ 6-17x ^ 2 +-14x 7 $) $ 7 $ egale. Gradul dividendului (polinomul $ 7x ^ 3 + 9x ^ 2-5x + $ 9) este egal cu 3. În această situație, atunci când gradul de divizorul divizibile mai mare măsură (7 $> $ 3) descompunerea formei (1) este posibilă numai în forma:
Răspuns. Private este 0, iar restul - $ 7x polinomul ^ 3 + 9x ^ 2-5x + 9 $.