Noi rezolva problemele tipice ale geometriei analitice

Luați în considerare principiul rezolvării problemelor pe acest subiect. „O linie dreaptă în plan, găsiți ecuația o linie dreaptă care trece printr-un anumit punct, găsirea punctelor de intersecție a Bisectoarele unghiuri, etc.“.

Luați în considerare următoarea problemă ca un exemplu

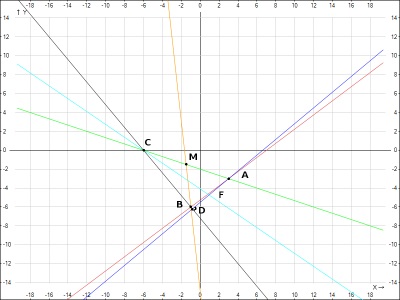
Exemplu: având coordonatele vârfurile triunghiului \ (ABC \) \ (A (3; -3); B (-1, -6) C (-6; 0) \)

1. Asigurați-ecuația de laturi ale triunghiului.
   
2. găsi ecuația
   
   
   
   1. înălțimea \ (AD \),
      
   2. median \ (BM \),
      
   3. bisector \ (CF \).
      
   
   
3. Crearea unui sistem de inegalități, soluții din care este mulțimea tuturor punctelor de un triunghi \ (ABC \).
   
4. Găsiți unghiul \ (B \) în radiani până la două cifre.
   
5. Fă un desen.
   

1. Asigurați-ecuația de laturi ale triunghiului. Pentru a compila ecuația laturilor triunghiului atinse starea problemei. În condiția dată coordonatele trei vârfuri ale triunghiului, adică pentru a compila ecuațiile liniilor \ (AB, BC, CD \) primesc 2 puncte prin care trec liniile. Pentru a utiliza linia de soluții de ecuații care trece prin cele două puncte având în vedere $$ \ frac = \ frac $$ unde \ ((x_1; y_1) \) - coordonatele primului punct cunoscut, \ ((x_2; y_2) \) - coordonatele unui al doilea punct cunoscut . Înlocuim coordonatele și de a obține ecuația liniei
   \ Directe (AB \). trece prin punctul \ (A (3; -3); B (-1; -6) \), formează ecuația $$ \ frac = \ frac => \ frac = \ frac => y = \ fracx- \ frac $ Am primit $ liniar ecuația \ (AB \). În ecuația notă directă panta \ (k_ = \ frac \), care este necesară în următoarele probleme.
   \ Directe (BC \). Ea trece prin punctul \ (B (-1, -6) C (-6; 0) \) formează ecuația $$ \ frac = \ frac => \ frac = \ frac => y = - \ fracx- \ frac $$ a primit ecuația \ liniar (BC \). În ecuație, observăm panta liniei drepte \ (k_ = - \ frac \), care este necesară în următoarele sarcini.
   \ Directe (AC \). trece prin punctul \ (A (3; -3); C (-6; 0) \) formează ecuația $$ \ frac = \ frac => \ frac = \ frac => y = - \-fracx 2 $$ Am primit ecuația unei linii \ (AC \). În ecuație, observăm panta liniei drepte \ (k_ = - \ frac \), care este necesară în următoarele sarcini.
   
2. găsi ecuația
   
   
   
   1. înălțimea \ (AD \). în ecuația înălțime cunoaștem coordonatele doar un singur punct - \ (A (3, 3) \), deci vom folosi linie dreaptă ecuație care trece printr-un anumit punct într-o anumită direcție. $$ y-y_0 = k_ (x-x_0) $$. unde \ ((x_0; y_0) \) - coordonatele unui punct cunoscut și \ (k_ \) - panta. În această ecuație, nu știm doar panta. Găsiți-l, pentru aceasta folosim proprietatea liniilor perpendiculare. \ Direct (AD \ bot BC \). Înregistrați proprietățile \ (k_ * k_ = -1 => k * _ (- \ frac) = -1 => k _ = \ frac \). Construirea ecuatia liniei \ (AD \) $$ y - (- 3) = \ frac (x-3) => y = \ fracx- \ frac $$
      
   2. median \ (BM \), pentru ecuația mediană în problema găsirii unui anumit punct de coordonate \ (B (-1; -6) \), și este de asemenea cunoscut faptul că mediana împarte direcția opusă în jumătate. Găsim coordonatele punctului \ (M \). Pentru aceasta se folosește formula coordonatele punctului care împarte intervalul \ (AC \) într-un raport predeterminat \ (\ lambda \), în cazul în care \ (\ lambda = \ frac = \ frac = 1 \), iar coordonatele \ ((x_1; y_1) (x_2; y_2) \) - coordonatele obiective care împarte punctul \ (M \) t.e.tochek \ (a (3; -3); C (-6; 0) \) substitut și pentru a primi $ $ x = \ frac = \ frac = - \ frac y = $$$$ \ frac = \ frac = - \ frac $$ primit coordonatele punctului \ (M (- \ frac; - \ frac) \). Am primit două puncte, prin care ecuația linie dreaptă pentru utilizare ecuație linie dreaptă care trece prin cele două puncte menționate \ (\ frac = \ frac \), vom înlocui coordonatele punctelor \ (B (-1; -6), M (- \ frac; - \ frac) \) și se obține $$ \ frac + 6> = \ frac + 1> => y = -9x-15 $$
      
   3. bisector \ (CF \), pentru a găsi ecuația utilizării bisectoarea unghiului bisector proprietatea triunghiului: bisectoarea interioară a unghiului triunghiului împarte latura opusă a colțului în segmente care sunt proporționale cu celelalte două laturi ale \ (\ frac = \ frac \), adică astfel, vom găsi factorul \ (\ lambda \), apoi utilizați formula pentru coordonatele punctului care împarte intervalul \ (AB \) într-un raport \ predeterminat (\ lambda \) și să găsească coordonatele punctului \ (F \) și coordonatele ultimului substitut derivate în ecuația liniei care trece prin cele două puncte specificate.
   Începem: găsi lungimea segmentelor \ (AC \), \ (BC \). $$ AC = \ sqrt = \ sqrt = \ sqrt = \ sqrt $$$$ BC = \ sqrt = \ sqrt = \ sqrt = \ sqrt $$ găsim acum coeficientul \ (\ lambda = \ frac = \ frac = \ sqrt > \). Noi găsim coordonatele punctului \ (F \) la coordonatele cunoscute ale punctele finale \ (AB \) \ (A (3; -3); B (-1; -6) \) $$ x = \ frac = \ frac >>> > $$$$ y = \ frac = \ frac >>>> $$ a obținut două puncte, prin care linia \ (CF \), pentru ecuația \ direct (CF \) utilizează linia dreaptă care trece ecuație prin cele două puncte definite \ (\ frac = \ frac \), înlocuim coordonatele punctelor \ (C (-6; 0) F (\ frac >>>>; \ frac >>>>) \) și se obține $$ \ frac >>> > -0> = \ frac >>>> + 6> => \ frac >>>>> = \ frac> + 6 + 6 * \ sqrt >>>>> => $$$$ \ frac >> = \ frac >> => $$$$ y = \ frac >> * (- 3-6 * \ sqrt>) => $$$$ y = - \ frac >>>> * x-18 \ frac >> >> $$
   

Fă un desen.