Să se dea un set arbitrar A și B.
Definiție: Intersecția seturi A și B este multimea A

A



Luați în considerare setul A și B în diagramă arată intersecția acestor seturi. Să:
1) stabilește A și B nu intră în relație unele cu altele.
Evident, în acest caz, A

2) stabilește A și B sunt în relația de egalitate.
apoi, A

3) stabilește A și B sunt în includere.
În cazul în care un




Eclozarea prezintă o multitudine de elemente aparținând A

4) stabilește A și B sunt în relația de intersecție.

Double hașurarea prezintă o multitudine de elemente aparținând A

Fie A = a; b>, B =. găsim o

Prin determinarea intersecția a două seturi A


Notă: Într-un discurs la funcționarea de intersecție corespunde cuvântului „și“. și fuziune a operațiunilor - cu „sau“.
Astfel, prin definiție, x





Intersecția mulțimilor A și B nu acele elemente nu sunt în A. sau B. Astfel, x





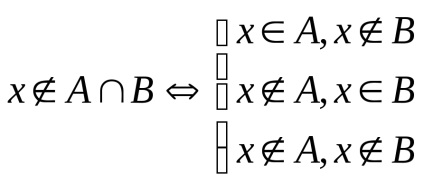
Notă. Funcționarea găsi asociației (intersecție) stabilește, de asemenea, numită asociație (intersecție).
seturi de scădere
Să se dea un set arbitrar A și B.
Definiție: Diferența dintre două seturi A și B este mulțimea A \ B. ale cărui elemente aparțin setului A, dar care nu fac parte din setul B.
A \ B = x | x


Vom arăta diferența în diagrama de seturi A și B. Fie:
1) stabilește A și B nu intră în relație unele cu altele.
Este evident că în acest sluchaeA \ B = A și B \ A = B.
2) stabilește A și B sunt în relația de egalitate.
3) stabilește A și B sunt în includere.
În cazul în care un



4) stabilește A și B sunt în relația de intersecție.
Eclozarea prezintă o multitudine de elemente aparținând A \ B.
Prin definiție, diferența dintre cele două seturi A \ B = a; b>. deoarece numai aceste elemente aparțin setului A și B set - nr.
Deoarece N


Notă: În cazul în care setul B este un subset al A. diferența A \ B este complementul multimea B pentru a seta A și este notat cu B
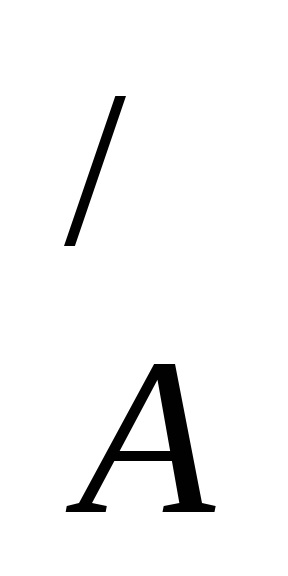


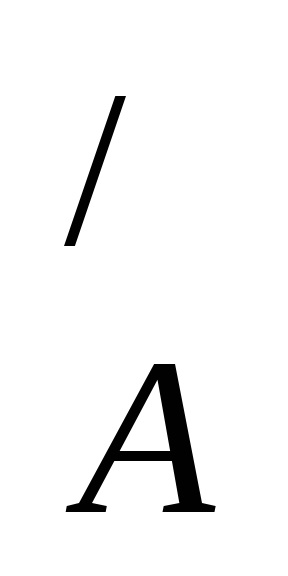
Dacă A - este setul universal (J), atunci diferența J \ B = B

1) Fie A = a; b>, B =. Dacă este posibil, pentru a primi adăugarea de B la A sau A la B.
Din moment ce un


Deoarece N


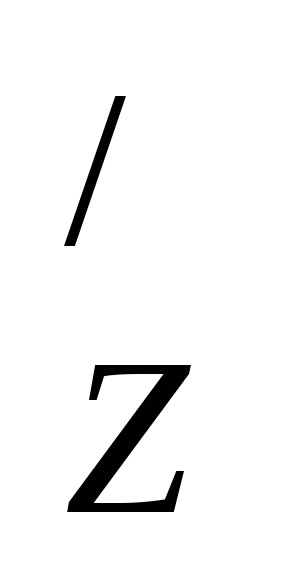

Notă: Pentru a defini un set de numere reale, se folosesc simboluri speciale: intervale numerice. De exemplu,
[A; b] = x | x



[A; b) = x | x



(A; b] = x | x


