sarcinile de distribuție asociate cu distribuirea resurselor cu privire la activitatea pe care trebuie să fie făcut. această clasă de probleme apar atunci când resursele disponibile nu sunt suficiente pentru a efectua fiecare operație modul cel mai eficient. Prin urmare, scopul de a rezolva problema este de a găsi o astfel de distribuție a resursei, în care fie minimizează costul total asociat cu performanța de muncă sau maximizată care rezultă din veniturile totale.
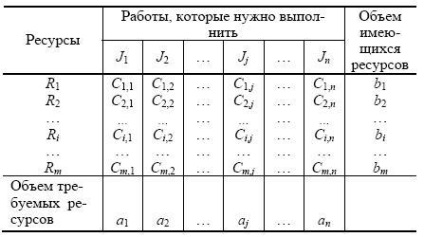
Cele mai multe sarcini pot fi reprezentate sub forma de distribuire a matricei conținută în tabelul 5.1.
Elemente Cij. stând în picioare în celulele matricei, costurile asociate sau a venitului, care corespunde alocarea unei unități de resurse Ri Jj de locuri de muncă. Valorile Cij pot fi independente și dependente.
De exemplu, costurile generate de numirea unui vehicul cu motor pe un anumit traseu de livrare de bunuri, nu depind de ce mașinile sunt atribuite altor servicii rute. În același timp, în diviziunea de distribuție (de exemplu, producția), de obicei, depinde de ce fondurile vor fi cheltuite de către alte departamente (de exemplu, vânzări). Teoria de distribuție se concentrează în principal asupra sarcinilor cu costuri independente și venituri. Acest lucru se explică nu prin faptul că astfel de sarcini sunt mai importante, dar numai pentru cei care sunt mult mai ușor de a construi un model și de a obține soluții.
În cazul în care costul (sau beneficiul) definit de resurse volum Hij I, Ji selectat pentru a efectua HijCij de muncă sunt egale, atunci avem o problemă de distribuție liniară.
Metode de bază pentru rezolvarea problemelor de distribuție, în special de programare, liniar, construit pe ipoteza că volumul resurselor disponibile (BI), cantitatea necesară (aj) și costurile (Ci, j) sunt cunoscute cu precizie.
În cazul în care volumul total al resurselor disponibile # 931; bi (i = 1 ... m) este egală cu cererea totală pentru ele # 931; aj (i = 1 ... n), atunci există o problemă de distribuție echilibrată (închis). În cazul în care, cu toate acestea, # 931; aj ≠ # 931; bi. atunci problema se numește dezechilibrat (deschis). În cazul în care resursele pot fi împărțite între locuri de muncă, unele de lucru se poate realiza prin utilizarea de diferite combinații de resurse. În cazul în care activitatea și resursele sunt măsurate în unități de la aceeași scară, aceste probleme sunt, de obicei denumite de transport sau de descompunere de activitate. În cazul în care activitatea și resursele sunt exprimate în unități diferite, atunci problema se numește o sarcină generală de separare. Astfel, problema de transport este un caz particular al problemei generale a distribuției.
Metodele de operare
Există unii furnizori de bunuri M. Cantitatea de bunuri disponibile de la furnizorii de A1. A2, ..., AM unități. Există N consumatori ai acestui produs; cererea lor este B1. B2. ..., unități BN. Cantitatea de inventar al bunurilor disponibile furnizorilor, egal cu suma cererii tuturor consumatorilor:
Cunoscut de costul unitar de transport de la fiecare furnizor pentru fiecare client (costul de transport maritim): Cij. i = 1, ..., M, j = 1, ..., N.
Este necesar pentru a face un plan de transport (cum, în cazul în care, și cât de multe unități put), astfel încât toate cererile au fost făcute, iar valoarea totală a tot traficul a fost minimă.
Să considerăm mai întâi soluția problemei de transport este închis, adică, atunci când suma tuturor ofertelor este egală cu suma tuturor rezervelor.
Explicați-l cel mai simplu mod ar fi un exemplu concret:
Exemplul 5.1. Cu patru depozite (CK1, CK2, CK3, CK4) livrarea mărfurilor în cele trei magazine (mg 1, MG2, MG3). În stoc TC1 are 40 de tone de produse pe stoc CK2 - 50 de tone de stoc TC3 - 60 de tone de stoc CK4 - 30 tone. A se păstra mg 1 necesare 60 de tone de mărfuri, magazin MG2 - 80 de tone, magazin MG3 - 40 de tone. Costurile (în vizuină. U), asociate cu transportul unei tone de mărfuri din fiecare depozit la fiecare magazin, sunt prezentate în Tabelul. 5.2.
Este necesar să se determine cât de multe dintre mărfurile care urmează să fie transportate de la fiecare depozit la fiecare magazin pentru a livra toate magazinele necesare cantități de produse cu costuri minime.
Această problemă poate fi reprezentată ca o problemă de programare liniară. Pentru a construi un model matematic al acestei probleme, introducem variabile Xij. i = 1, ..., 4, j = 1, ..., 3, indicând cantitatea de mărfuri transportate din depozitul i-lea magazin-j-lea.
În depozite dispune de 180 de unități de mărfuri; 180 de unități de mărfuri, de asemenea, magazine necesare. Prin urmare, pentru a satisface cererea de toate magazinele trebuie să scoată bunurile din depozitele de ansamblu. Restricțiile care exprimă această cerință sunt după cum urmează:
Fiecare magazin trebuie să obțină la fel de mult ca și produs are nevoie. Restricțiile care exprimă această condiție, următoarele:
Deoarece variabilele indică numărul de mărfuri transportate, acestea sunt supuse cerinței de non-negativitate:
Funcția obiectiv este costul de conformare cu tot traficul:
Această problemă poate fi rezolvată prin metoda simplex, precum și orice problemă de programare liniară. Cu toate acestea, o astfel de soluție ar fi destul de complicată din cauza numărului mare de variabile și constrângeri incluse în modelul matematic al problemei. Pentru a rezolva problemele de acest gen, există metode speciale, mai simple.
În rezolvarea problemei de transport este convenabil de a utiliza tabelul de calcul care conține costul transportului, stocurilor de mărfuri de la furnizori și valoarea cererii de consum. În cursul rezolvării problemei în valoarea înregistrată a transporturilor (valori ale variabilelor xij), precum și valorile auxiliare folosite pentru a rezolva problema. Tabel de calcul pentru Exemplul 5.1 este prezentată în Tabelul 5.3.