Aflați piramida descrie în diferite poziții.
Desenați cubul pe termen de colț. Construiți pe fiecare pătrat din baza piramidei verticale și orizontale cub.
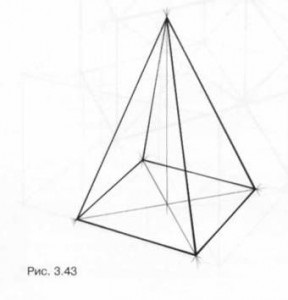
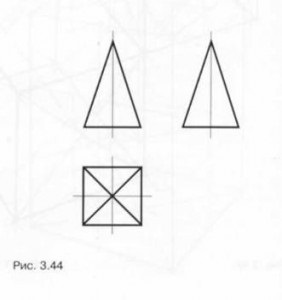
Să considerăm o piramidă în Fig. 3,43 și proiecția sa ortogonală în Fig. 3.44. Baza unei piramide tetraedrice este un pătrat. fețele sale laterale - aceleași triunghiuri. Înălțimea piramidei în raport cu partea de bază a pătrat determină proporția sa (ridicat sau ghemuit).
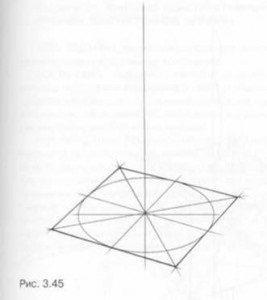
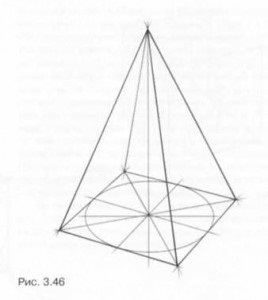
Pentru a începe construcția piramidei trebuie să fie în picioare, cu o imagine de bază pătrată. Prin punctul de intersecție al diagonalelor sale glisează pe verticală, care a anulat un segment egal cu înălțimea piramidei (fig. 3.45). Combinarea vertex astfel obținut dintr-o piramidă cu un pătrat vârfuri de bază se obține un desen în perspectivă a piramidei cu patru laturi (Fig. 3.46). Construcția unei piramide cu baza pătrată verticală este realizată în aceeași secvență.
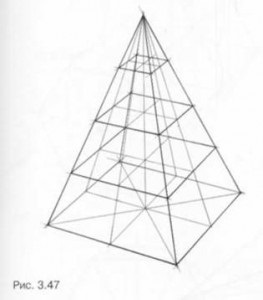
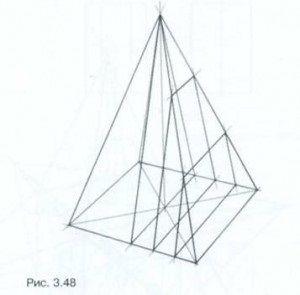
plane secționate piramidale paralel cu baza, - pătrate ale căror dimensiuni depind de poziția planului de tăiere - (. Figura 3.47) este mai aproape de partea superioară a dimensiunii piramidei secțiunilor transversale este mai mică decât în partea de jos. Secțiunea transversală perpendiculară pe baza piramidei, care trece prin vertex și linia medie de bază pătrată, este un triunghi. Toate celelalte secțiuni ale piramidei paralel cu acesta - trapezoidală, care este egală cu latura bazei mari a bazei pătrat minim - variază în funcție de poziția planului secțiunii (Figura 3.48.). În construirea acestor secțiuni amintim că laturile trapezelor sunt paralele cu înălțimile triunghiuri din fețele laterale.
piramide de desen liniar constructive
piramide de desen liniar constructive
piramide de desen liniar constructive
piramide de desen liniar constructive
piramide de desen liniar constructive
piramide de desen liniar constructive
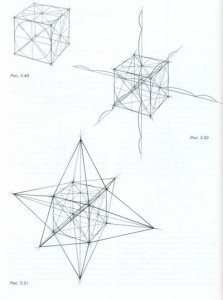
Acum, că bine ați studiat secvența de construcție a piramidei și planurile sale de secțiune ale diferitelor direcții, pentru a trece îndeplini sarcinile de bază. Desenați cub (fig. 3.49). Centrarea pe diagonală toate cele șase fețe ale cubului și desena o linie care leagă centrele de pătrate opuse. Pune pe aceste linii înălțimea piramidelor (fig. 3.50). Toate cele șase piramide sunt aceeași înălțime (1.5a, în cazul în care o - marginea cubului), dar cifra înălțimii lor au dimensiuni diferite. Pentru a determina înălțimea piramidei diferitelor prevederi din diverse segmente sunt folosite ca unitate de măsură. De exemplu, în determinarea înălțimii pe verticală a piramidelor este o unitate de măsură a segmentului vertical limitat de puncte de centre orizontale ale fețelor de cub. Pentru înălțimea piramidelor orizontale astfel de unități sunt segmente de linii drepte care trec prin centrul cubului, și au aceeași direcție ca și înălțimea determinată. Astfel, orice cifră care se bazează pe corpul geometric, acționează ca o linie tridimensională cubi prin intermediul cărora este posibil să se determine sau măsura lungimile segmentelor aflate în trei direcții reciproc perpendiculare. Definirea nodurile punct al piramidelor, ia în considerare, de asemenea, segmentele de reducere pe termen lung. Conectați partea de sus a șase piramide cu vârfuri terenuri pătrate (fig. 3.57).
piramide de desen liniar constructive