Derivative și diferențială
Să presupunem că funcția y = f (x) definit pe X. interval Ia un punct
x Î H. Să ne dea o valoare increment x Dx ¹ 0, atunci funcția primește increment D y = f (x + Ax) - f (x).
Derivata funcției y = f (x) se numește limita raportul funcției increment la incrementarea argumentul atunci când acesta din urmă tinde la zero (dacă există această limită).
Derivatul de asemenea, notat y „și dy / dx.
semnificația geometrică a derivatului
Pentru a înțelege semnificația geometrică a derivatului, ia în considerare problema tangenta.
Să considerăm un grafic plan al unei funcții continue y = f (x) (a se vedea. Figura 3.1).
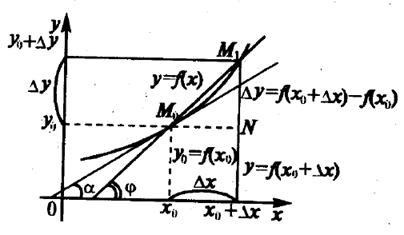
Construim o tangentă la această curbă la punctul M0 (x0. Y0). Mai întâi trebuie să se definească conceptul de tangenta. Pentru acest argument vom da o Dx increment x0 și treci pe curba y = f (x) dintr-un punct
M0 (x0. F (x0)) la punctul M1 (x0 + Ax, f (x0 + Ax)). Desenați o trecere M0 M1. Sub tangenta la curba y = f (x) realizează poziția limită a aproximarea secantă M0 M1 M1 la un punct la punct M0. și anume când Dh®0.
tăiere Corner factor M0 M1 (tangenta unghiului de înclinare al acestei linii j la abscisă) pot fi găsite din DM0 M1 N :. Apoi panta tangentei (tangenta unghiului a) este egal.
Astfel, derivata funcției este panta tangentei la graficul de axa x (coeficientul unghiular tangențial).