Măsurătorile directe sunt împărțite în echilibru multiple și inegale. Fundamentele teoretice și tehnica combinarea rezultatelor măsurătorilor inegale discutate în detaliu în [3]. La fel numite exact măsurătorile sunt efectuate prin intermediul aceeași precizie de măsurare a uneia și procedura de Lee în condiții ambiante constante. Atunci când măsurătorile la fel de exacte MSE rezultatele tuturor seriilor de măsurare sunt egale.
Înainte de a procesa rezultatele măsurătorii, este necesar să se asigure că datele din eșantionul procesat este controlată statistic, grupate în jurul același centru și au aceeași variație. Schimbări de rezistență sunt adesea evaluate în mod intuitiv pe baza observațiilor pe termen lung. Cu toate acestea, există metode matematice pentru a rezolva această problemă - așa-numitele metode de testare omogenitate [3]. În ceea ce privește măsurătorile de uniformitate observate grupe de cazuri, semnele necesare, care constau în evaluarea mediei echidistantă și variația între ei.
Diferențele de validare între estimările varianțele ale rezultatelor de măsurare distribuite în mod normal efectuate de criteriul R.Fishera dacă există două grupe de observații și criteriul M.Bartletta dacă grupurile mai mari. criteriu Fisher a considerat în cap. 5.
Rezultatele de prelucrare a sarcinii de măsurători multiple este de a găsi estimările și valoarea măsurată a intervalului de încredere, care este valoarea sa reală. Prelucrarea trebuie efectuată în conformitate cu GOST 8.207-76 „GSI. Măsurătorile directe cu mai multe observații. Metode de prelucrare a rezultatelor observațiilor. Dispoziții generale.“
Informațiile inițiale pentru procesarea unui număr de n (n> 4) măsurători x1. x2. HG xn. care exclud cunoscute erori sistematice - eșantionare. Numărul n depinde de cerințele pentru acuratețea rezultatului, precum și posibilitatea reală de a efectua măsurători repetate.
Secvența de prelucrare a rezultatelor măsurătorilor directe multiple constă în mai multe etape.
Determinarea estimărilor punctului de distribuire a rezultatelor măsurătorilor. În această etapă, se determină:
• aritmetică valoarea x este valoarea măsurată de formula (6,8);
• rezultatul măsurării MSE Sx prin (6.11) sau (6.12);
• Abaterea standard a valorilor medii aritmetice Sx # 773; prin (6.10). În conformitate cu criteriile discutate în Cap. 7, erori grosolane și greșelile sunt eliminate, urmate de estimările recalculați de aritmetică medie și deviația standard. În unele cazuri, pentru identificarea mai fiabile a rezultatelor măsurătorilor legii de distribuție poate fi determinată prin alt punct de evaluare: asimetrici, kurtosis și kontrekstsess, raportul entropie.
Determinarea legii distribuției rezultatelor măsurătorilor sau erori de măsurare aleatoare. În al doilea caz de mostre de măsurători x1. x2. x3 -. xn sunt transferate pentru a proba abateri de la media aritmetică DH1. DH2. DH3. DHN. unde Dxi = xi - x # 773;.
Primul pas în identificarea legii de distribuție este de a construi pe rezultatele corectate de măsurare xi. unde I = 1, 2. n, seria de variație (selecție ordonate) și yi. unde yi = min (xi) și yn = max (xi). Într-o serie de variații ale rezultatelor măsurării (sau abatere de la media aritmetică) sunt aranjate în ordine crescătoare. Mai mult, acest interval este împărțit la numărul optim m, sunt intervalele de grupare, în general, identice de lungime h = (y1 + in) / m.
Problema determinării numărului m optim de intervale de gruparea considerată într-un număr de studii, revizuite în [4]. Optimul este un număr de intervale m în care posibilele date maxime de uniformizare fluctuație aleatoare însoțită de distorsiune minimă a netezirea curbei în sine distribuția dorită. Pentru aplicații practice, se recomandă utilizarea propusă în [4] expresie mmin = 0,55n 0,4 și Mmax = 1,25n 0,4. sunt pregătite pentru cele mai frecvent întâlnite în practică cu distribuții aplatizării fiind în intervalul 1.8-6, adică de uniforma la distribuirea Laplace.
Valoarea necesară a m ar trebui să fie în intervalul de până la mmjn Mmax. impar, ca în cazul unei distribuții simetrice chiar m peakedness sau histogramă bimodală în centru sunt două coloane înălțime egală, și o curbă de distribuție mijlocie aplatizate în mod artificial. Dacă histograma de distribuție bimodală în mod clar, numărul de coloane poate fi crescută de 1,5-2 ori pentru fiecare dintre cele două vârfuri au reprezentat intervale de aproximativ m. Valoarea obținută a lungimii intervalului de grupare h este întotdeauna rotunjit în sus, în caz contrar ultimul punct este în afara intervalului extreme.
intervale de grupare suplimentară determinată de date experimentale ca D1 = (y1 y1 + h.); D2 = (y1 + h, y1 + 2h);. ; Dm = (yn - h, in), și a contoriza numărul de accesări nk (frecvență) a rezultatelor măsurătorilor în fiecare interval de grupare. Suma acestor numere trebuie să fie egal cu numărul de dimensiuni. Valorile obținute sunt calculate de probabilitatea ca rezultatele măsurătorilor (frecvențe relative) în fiecare interval de grupare cu formula pk = nk / n, unde k = l, 2. m.
Calculele fac posibilă construirea unei histograme, poligon și o curbă cumulativă. Pentru a construi o histogramă a rezultatelor observațiilor x axa (Fig. 8.1, a) depuse intervale dk, în ordine crescătoare și pe fiecare interval construit pk înălțime dreptunghi. Zona închisă sub grafic, Proporțional / ionalna n numărul de observații. Uneori, înălțimea dreptunghiului stabili empiricheskoy variind pk densitate de probabilitate = Pk / Dk = nk / (NDK), care este o estimare a densității medii în intervalul Dk. În acest caz, zona de sub histograma este egală cu unu. Prin creșterea numărului de intervale și de a reduce în mod corespunzător histograma lungimea lor se apropie din ce în ce o curbă lină - graficul densității de probabilitate. Trebuie remarcat faptul că, în unele sluyaaev produc estimat echilibrarea histogramă, care arată tehnica în [4]
Poligon este o curbă poligonală care leagă bazele superioare de mijloc ale fiecărei coloane histogramă (vezi. Fig. 8.1, a). Este mai clar decât histograma reflectă forma curbei de distribuție. În afara histograma pe dreapta și pe stânga există și spații goale, în care punctele corespunzătoare punctelor lor de mijloc se află pe axa x.
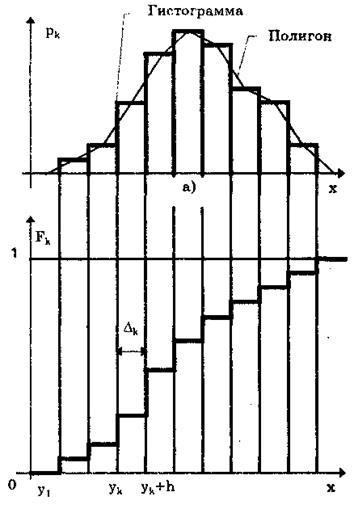
Fig. 8.1. Gistonramma, poligon (a) și curba cumulativă (b)
Aceste puncte atunci când se construiesc poligon interconectate prin segmente de linie dreaptă. Ca rezultat, împreună cu axa x formând o figură închisă, o zonă în conformitate cu regula de normalizare trebuie să fie egală cu unitatea (sau numărul de observații utilizând frecvențele relative).
Curba cumulativă a - un grafic al funcțiilor de distribuție statistică. Pentru a construi axial de observații x (Fig. 8.1,6) stabilește intervalele dk în ordine crescătoare numerică și de a construi pe fiecare înălțime dreptunghi interval
Valoarea Fk se numește frecvența relativă cumulativă, și valoarea nk - frecvența cumulativă.
În funcție de tipul de reprezentare grafică poate fi estimată dreptul de distribuție a rezultatelor măsurătorilor.
Evaluarea distribuției legii pe criterii statistice. Dacă numărul n> 50 observații pentru a identifica legea de distribuție folosind testul Pearson (chi-pătrat cm. 8.1.2) sau Mises criteriu Smirnov (w2). La 50> n> 15 pentru verificarea normalității legii de distribuție se aplică un criteriu compozit (d-test) dat în GOST 8.207-76. pentru n <15 принадлежность экспериментального распределения к нормальному не проверяется.
Determinarea limitelor de încredere ale erorii aleatorii. Dacă în măsură să identifice legea de distribuție a rezultatelor măsurătorilor, folosindu-l sunt factorul zp cuantila pentru o anumită valoare a probabilității de încredere P. În acest caz, limitele de încredere ale erorii aleatoare A = ± S zp -.
Definirea limitelor de rezultat neexcluse măsurarea q erori sistematice. În aceste limite rezultate realizeze metode non-statistice limitele intervalului în interiorul căruia este o eroare reziduală. Este format dintr-un număr de componente: în mod obișnuit, metoda și mijloacele de măsurare eroarea și eroarea subiectivă. Border neexcluse eroare sistematică sunt luate pentru a fi limita de eroare de bază și suplimentare tolerabil de instrumente de măsurare în cazul în care acestea sunt componente aleatorii sunt neglijabile. Acestea sunt rezumate în conformitate cu regulile discutate în Sec. 9.2. Nivelul de încredere în determinarea limitelor 6 este egal cu nivelul de încredere este utilizat pentru găsirea limitelor de eroare aleatoare.
Determinarea limitelor de încredere ale erorilor de măsurare rezultat Dp. Această operație se realizează prin adăugarea deviația standard a componentei aleatoare Sx # 773; și se învecinează cu q componenta reziduală în funcție de raportul q / Sx # 773; în conformitate cu normele stabilite în secțiunea. 9.4.
Pentru a salva un rezultat de măsurare. Rezultatul măsurătorilor este scris sub forma x = x # 773; ± Dp la un nivel de încredere de P = P. În absența unei componente de eroare de date ale funcției de distribuție a măsurătorilor sunt în forma x, S-, n, 8 la un nivel de încredere de P = Pd.