Chiar si sef primitiv a dat seama că o duzină de vânători „probabil“ a lovit sulița de bizon este mult mai mult decât unul. Prin urmare, am vânat apoi în mod colectiv.
Superficial ar putea crede că o astfel de vechi polkovod-tzu, ca Alexandru cel Mare sau Dmitry Donskoi, în curs de pregătire pentru luptă, să se bazeze doar pe vitejia și abilitatea de soldați.
Fără îndoială, ei sunt baza observațiilor și a experienței de conducere militară au putut evalua cumva „probabilitatea“ întoarcerii sale „scut“ sau „la bord“, au știut când să lupte, când să-l evite. Dar ei erau încă foarte departe de teoria probabilității.
Mai târziu, cu experiență, oamenii din ce în ce a început să-și planifice evenimentele eveniment Nye - observații și experimente, pentru a le clasifica iskho-dy imposibil, posibil și credibil. El a observat că accidentele nu sunt atât de rar rula obiectiv regularități-Ness. Aici este o experiență simplă - arunca o monedă. strat Pierderea de arme sau de numere, desigur, fenomen pur accidentală. Dar, de multe ori tragerea la sorți normală moneda se poate observa că apariția stemei are loc în aproximativ jumătate din cazuri. Deci, rezultatele aruncări de monede, cu toate că fiecare dintre ele este etsya eveniment aleator, care se repetă de repetiție aservită HN drept obiectiv. Pentru cei cu o înclinație pentru IP-traseu, există tentația de a acumula mai multe din legile dimensiunilor și să încerce să construiască o teorie a acestora.
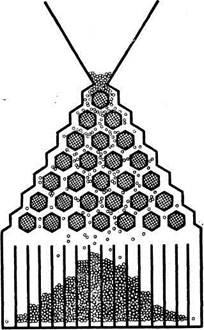
Luați în considerare un alt, de exemplu mai complicat - Experiment cu așa-numitul bord Galton (figura 6.). Consiliul de credință plasat-tikalno. Din rola bile de oțel rezervor superior (în secțiunile cad) în jos și se acumulează în orbite inferioare.
Fiecare șirag de mărgele, se confruntă pe calea următoare Px consecință, deviază, sau la stânga sau la dreapta, și apoi cade în jos. Mingea, desigur, pot cădea în oricare dintre sloturi.
Între timp, poziționarea corectă a bile (simetrice, în care cuiburilor centrale sunt multe, dar foarte puține), repetate de la prima la experimente pentru experiment, dovezile Ube-clusive a sous-existenței distribuției obiectiv-Kona. Când mingea mult, ei spun că acestea sunt distribuite prin lege pe termen normal.
Astfel, sansa poate fi sub-dregeau regularități-Cham relativ simple și mai complexe. Dar întrebarea este, în cazul în care este matematica, în cazul în care problemele de matematica?
Cele mai interesante pentru probleme pe-Chin de teoria probabilităților a apărut în domeniul jocurilor de noroc-TION, deși formarea principiilor teoriei probabilității spo-sobstvovali clarifica, de asemenea, durata vieții, numărul populației, practica, asigurare-TION. Prin jocuri de noroc atribuite aruncarea hex igral-TION de os. [1] Pe-exemplu, în aruncarea cu două panglica-dificil Tei ( „pericol“) este apariția unui total de două sau două puncte ale celor doisprezece.
După aproape cincizeci de ani, un alt matematician italian D. Cardano (1501-1576) supuse argumentele Pacioli fair-urlet de critici, dar el a sugerat că decizia eronată.
A fost nevoie de încă 100 de-plus de ani, iar în 1654 problema a fost pe în cursul corespondenței între doi matematicieni restante tsuzskimi-a rezolvat sfârșitul Fran B. Pascal (1623-1662) și Fermat (1601-1665).
Pentru prima dată bazele teoriei probabilității au fost dispuse URMA quently de matematicianul francez Pierre Simon de Laplace (1749-1827), în cartea sa „Teoria analitică a probabilității.“
Laplace nu putea să prevadă că va dura câteva zece Lety și de interes în teoria probabilității de a cădea. Și, de fapt, ce sa întâmplat. În a doua jumătate a secolului al XIX-lea și XX matematica secolului Neko-torye nu mai este interesat în teoria probabilității ca o disciplină matematică.
Cum se explica aceasta indiferenta a unor matematicieni din teoria probabilității? Motivele sunt multe. Dar aici vom deschide numai unul.
Probabilitatea evenimentului a fost determinată de Laplace după cum urmează:
unde n - numărul total de evenimente în mod egal, o m - numărul acestor evenimente are loc atunci când rezultatul dorit ( „favorizarea eveniment“).
Se pare că totul este în ordine - la definiția lui Laplace de evenimente de probabilitate nu a putut găsi vina. Dar întrebarea este: când și ce evenimente aleatoare pot fi considerate la fel de posibil?
Un copil se naște. Băiat sau fată - se pare evenimente la fel de probabil (unul dintre cei doi, la fel ca în aruncarea unei monede). Dar se pare că statisticile de naștere nu sunt în întregime în concordanță cu noastre „cred.“
Acesta poate fi, de exemplu, după cum urmează:
Dacă la momente diferite în diferite țări, mai mulți băieți se nasc decât fetele, astfel încât probabilitatea de nașterea unui băiat sau fată inegala: probabilitatea evenimentului „copil băiat“ mai.
Să ne amintim tragerea la sorti (a se vedea. Deasupra). În cazul în care avem încredere că probabilitatea de capete, atunci când flipping repetate la infinit, este egal?
Situația de fapt din care reiese că realitatea obiectivă nu coincide neapărat cu omul „pare“, au cauzat îndoieli în legitimitatea conceptului de „evenimente la fel de posibile.“ A existat o nevoie de a „re-examina“ probabilitatea ca tu-calculat prin ecuația Laplace. experimente.
apărat cu înverșunare poziția teoriei probabilității românești de mate-Matic. În 1846, Academia St. Petersburg de Științe a publicat o carte V. Ya. Bunyakovskogo (1804-1889), intitulat "Fundamentele teoriei-mate matic de probabilitate." Acesta a fost primul manual românesc pe teoria probabilității. Pe ea a mers, si restante subiecte ma românesc P. L. Cebîșev. Deși el a scris pe teoria probabilității nu este atât de mult de lucrări, dar ele rămân extrem de important ZNA-chenie până în prezent. Așa-numita inegalitatea P. L. Chebysheva pentru intrat vreodată în vistieria științelor matematice.
Elev P. L. Chebysheva A. A. Markov a dezvoltat lucrări Uchi sale Tell. A Lui este slava Descoperitorul importante aplicații ale teoriei probabilității - teoria probabilității, sau procese stocastice.
Moștenirea matematicienilor români a fost dezvoltat în lucrările sovietice matematicieni EE Slutsky, SN Bernstein, AJ Khinchin, Y. Linnik și în special Academicianul AN Kolmogorov. AN stabilită Kolmogorov școală sovietică teoriei probabilitatilor a câștigat recunoașterea și astăzi are o poziție de lider în domeniul științei mondiale.