Inegalitatea - două numere sau expresii matematice, legate de unul dintre personaje:> (mai mare decât în cazul inegalităților stricte) <(меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Inegalitatea este liniar în aceleași condiții ca și ecuația: ea conține numai variabile în primul grad, și nu conține produse de variabile.
Soluție inegalităților și sisteme de inegalități liniare liniare este indisolubil legată de sensul lor geometrică: soluție inegalitate este un semiplanului, plan care împarte întreaga linie a cărei ecuație set inegalități liniare. Această semiplanului, iar în cazul unui sistem de inegalități liniare - o parte a planului delimitat de mai multe linii, necesare pentru a găsi desenul.
Soluția de sisteme de inegalități liniare cu un număr mare de variabile, reduce multe provocări economice, în special, o problemă de programare liniară. care este necesară pentru a găsi maximul sau minimul unei funcții.
Să examinăm primele inegalități liniare pe plan. Luați în considerare o inegalitate în două variabile și:
unde - coeficienții variabilelor (unele număr), - termenul constant (ca număr).
O inegalitate cu două necunoscute, precum ecuația are un număr infinit de soluții. Soluția acestei inegalitate noi numim o pereche de numere care satisfac această inegalitate. Geometric soluția set inegalității este descris ca un semiplan delimitat de drepte
care va fi numit linia de delimitare.
Pasul 1. Construiți liniile care delimitează setul soluție de inegalitate liniară
Pentru aceasta avem nevoie să știm oricare două puncte ale liniei. Ne găsim punctele de intersecție cu axele de coordonate. Ordonata punctului de intersecție A este egal cu zero (figura 1). Valorile numerice de pe axele din această figură se referă la exemplul 1, care Să examinăm imediat după aceea tereticheskogo excursie.
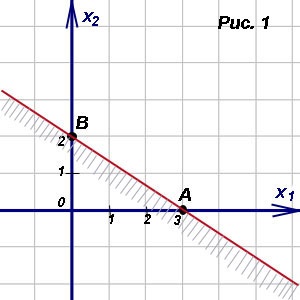
Abscisa găsi, ca un sistem de ecuații rezolvarea directă cu axa.
Găsim intersecția axei: