Deoarece proprietățile sistemului sunt exprimate prin valorile ieșirilor sale, starea sistemului poate fi definit ca un vector de valori ale variabilelor de ieșire Y = (y1. Ym). Am menționat mai devreme (a se vedea. Întrebarea №11), ca printre componentele vectorului Y, în plus față de direct variabilele de ieșire par arbitrare de la ei.
Comportamentul sistemului (procesul) poate fi reprezentat în diferite moduri. De exemplu, atunci când variabilele m de ieșire poate fi următorul proces formează imaginea:
o sub forma unui tabel de variabile de ieșire pentru valori discrete ale momentelor de timp t1, t2 ... tk;
Oa m parcele în yi coordonatele - t, i = 1, ..., m;
o grafic în sistem m-dimensional de coordonate.
Să considerăm acest din urmă caz. Sistemul m-dimensional de coordonate, fiecare punct-Corespunzător există anumit statut de sistem.
Setul de stări posibile ale sistemului Y (y ∈ Y) sunt considerate ca spațiu de stat (sau spațiul de fază) a sistemului, iar coordonatele acestui spațiu se numește coordonatele de fază.
În spațiul de fază a fiecărui element determină complet starea sistemului.
Punctul care corespunde stării actuale a sistemului, numit o fază sau reprezentantul, punct.
Faza traiectorie - o curbă care descrie punctul de fază atunci când starea sistemului neperturbat (la influențe externe constante).
Un set de traiectorii de fază corespunzătoare tuturor condițiilor inițiale posibile se numește un portret fază.
Faza portret surprinde doar direcția de viteza de fază a punctului și, prin urmare, reflectă doar o imagine calitativă a dinamicii.
Construiți și vizualiza portretul de fază poate fi numai pe planul, adică. E. Atunci când spațiul de fază este bidimensional. Prin urmare, metoda din spatiul fazelor, care în cazul unui spațiu faze bidimensional este numit de planul de fază, este utilizată în mod eficient pentru studiul sistemelor de ordinul doi.
Faza de coordonate plan este planul în care axele de coordonate depuse oricare două variabile (coordonate de fază), definind fără echivoc starea sistemului.
Fixe (staționare sau speciale) sunt punctele a căror poziție în portretul de fază nu se va schimba odată cu trecerea timpului. termeni specifici reflectă poziția egal la echilibru.
Folosind planul de fază este justificată, deoarece starea sistemului este determinată de cel puțin două variabile: valoarea producției sistemului și rata de schimbare de coordonate. În cele ce urmează, presupunem că axa x a planului de fază a cheniya întârziat ieșire ZNA-coordonatele y1 = y și axa ordonatei - rata schimbării y2 = y \ „(figura 1.).
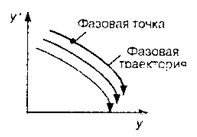
Fig. 1. Faza EXEMPLU portret.
Apoi traiectoriile fază a sistemului neperturbat avem următoarele proprietăți:
o printr-un singur punct al planului de fază trece doar o singură cale;
o în partea superioară se mută punctul de jumătate de imagine de la stânga la dreapta, iar în partea de jos - funingine, respectiv vice-versa;
o la abscisă derivat dy2 / dy1 = ∞ pretutindeni, cu excepția la punctele de echilibru, astfel încât traiectoriile de fază se intersectează axa abscisei (în punctele nesingulare) la unghiuri drepte.
Sistemul liniar are un punct singular unic - originea. tems neliniara B sunt caracterizate printr-o mare varietate de portrete de fază - acestea pot avea câteva puncte specifice.