Este necesar să se definească ceea ce este înălțimea paralelogramului.
Acest lucru realizat perpendicular prin orice punct al laturii paralelogram a liniei ce conține latura paralelă opusă. De obicei, înălțimea exploatației de vârfurile paralelogram. Deoarece paralelogramul are două perechi de laturi paralele, are o înălțime de două lungimi diferite.
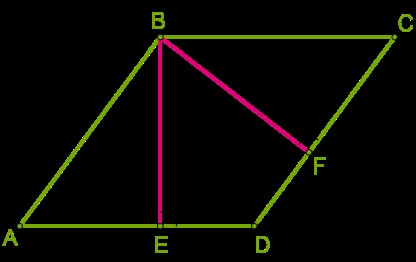
Înălțimea \ (BE \), The prestată între laturile lungi mai scurte decât înălțimea \ (BF \), realizat între laturile scurte.
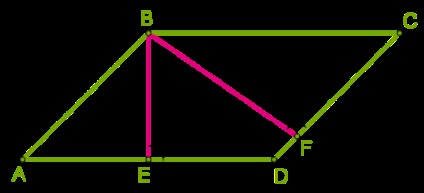
Deoarece partea de rombul sunt aceleași, înălțimea rombul sunt aceleași ca \ (BE = BF \).
Zona arbitrara a unui paralelogram
Suprafața unui paralelogram este egală cu produsul dintre înălțimea părților la care a avut loc înălțime.
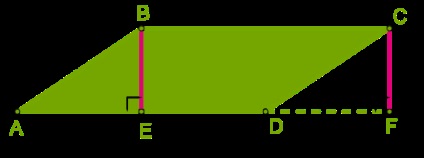
Desenați înălțimea celor două vârfuri \ (B \) și \ (C \) la latura \ (AD \).
Triunghiurile dreptunghiulare \ (Abe \) și \ (DCF \) sunt egale (egale ipotenuza ambele părți opuse ale paralelogramului și picioarele egale ale distanței dintre liniile paralele).
Paralelogram \ (ABCD \) și dreptunghi \ (EBCF \) - egal, deoarece acestea constau în cifre egale:
S ABCD = S Abe + S EBCD S EBCF = S EBCD + S DCF
Prin urmare, aria paralelogramului este definită ca fiind la fel ca și o zonă de dreptunghi:
S EBCF = BE ⋅ BC S ABCD = BE ⋅ BC = BE ⋅ AD
Dacă notăm partea printr \ (a \), înălțimea prin \ (h \), atunci:
S n - c = a ⋅ h
Pentru a determina aria unui paralelogram poate fi folosit latura scurtă și înălțimea, conected pe latura scurtă.
Diagonalele unui romb la intersecția împărțită la doi, ele sunt perpendiculare și se împarte rombul în patru triunghiuri egale în unghi-dreapta.
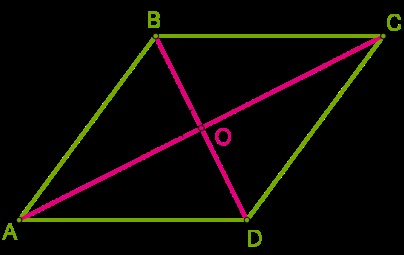
S ABCD = 4 ⋅ S ABO = 4 ⋅ BO ⋅ AO 2 = 2 ⋅ BO ⋅ AO