Figura prezintă construcția unui grafic sine pe intervalul.
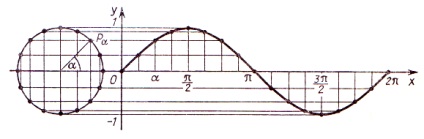
Luați în considerare proprietățile de bază ale funcției y = sinx:
2) un set de valori ale diferenței
3) este o funcție impar. graficul este simetric în jurul originii (0, 0).
4) funcție periodică. Cea mai mică perioadă pozitivă este
5) Funcția grafic intersectează axa x (zerouri) la punctele
6) Funcția grafic intersectează axa Oy la (0, 0).
7) Funcția ia valori pozitive în intervalele
8) Funcția ia valori negative pe intervalele
9) Funcția este în creștere pe intervalele
10) Această funcție este în scădere pe intervalele
11) Puncte minime:
12) maximum de puncte:
13) Graficul funcției este o undă sinusoidală
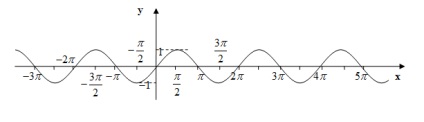
funcţia cosinus
Graficul este obținut din cosinus sine generată de translație paralelă cu o distanță spre stânga.
2) un set de valori ale diferenței
3) este o funcție chiar. grafic simetric față de axa y.
4) funcție periodică. Cea mai mică perioadă pozitivă este
5) Funcția grafic intersectează axa x (zerouri) la punctele
6) Funcția grafic intersectează axa Oy la (0, 1).
7) Funcția ia valori pozitive în intervalele
8) Funcția ia valori negative pe intervalele
9) Funcția este în creștere pe intervalele
10) Această funcție este în scădere pe intervalele
11) Puncte minime:
12) maximum de puncte:
13) Graficul funcției este un cosinus
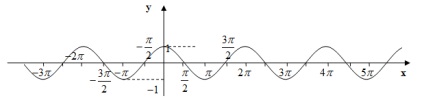
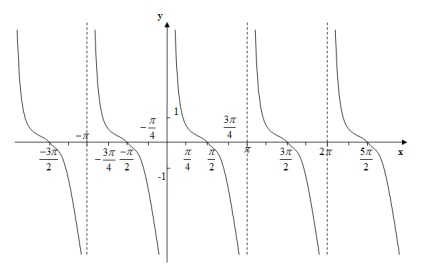
funcţia tangentă
3) este o funcție impar. graficul este simetric în jurul originii (0, 0).
4) funcție periodică. Cea mai mică perioadă pozitivă este
5) Funcția grafic intersectează axa x (zerouri) la punctele
6) Funcția grafic intersectează axa Oy la (0, 0).
7) Funcția ia valori pozitive în intervalele
8) Funcția ia valori negative pe intervalele
9) Funcția este în creștere pe intervalele
10) decalaje în scădere sunt absente.
11) fără puncte minime.
12) Puncte nr maxim.
13) Graficul funcției este tangensoida:
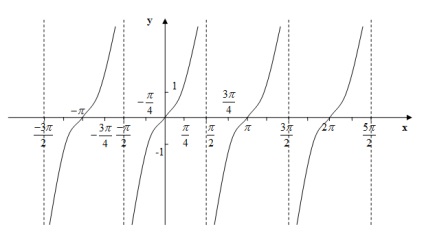
funcţia cotangentă
3) este o funcție impar. graficul este simetric în jurul originii (0, 0).
4) funcție periodică. Cea mai mică perioadă pozitivă este
5) Funcția grafic intersectează axa x (zerouri) la punctele
6) Funcția nu se intersectează axa Oy.
7) Funcția ia valori pozitive în intervalele
8) Funcția ia valori negative pe intervalele
9) Funcția nu crește intervalele.
11) fără puncte minime.
12) Puncte nr maxim.
13) Graficul funcției este kotangensoida:
elemente de epocă
1) În cazul în care T - perioada de bază a funcției y = f (x). numărul perioadei principale a funcției y = f (ax). în cazul în care un - orice număr pozitiv.
2) Dacă o funcție periodică y = f (x) și y = g (x) au aceeași perioadă T, atunci suma lor, diferența și produsul va avea, de asemenea, o perioadă T.
3) În cazul în care o funcție periodică y = f (x) și y = g (x) au perioade comparabile T1 și T2. acestea au o perioadă comună.
4) Perioada unei funcții compozit y = g (f (x)) coincide cu perioada funcției y = f (x).