poliedre semiregulate sunt o extensie naturală a poliedre regulate. Acest poliedre convexe ale cărui fețe sunt poligoane regulate - probabil cu un număr diferit de laturi, și în fiecare nod același număr de fețe. Cele mai multe dintre ele au fost descoperite de Arhimede. Dar ele sunt deschise și în secolul XX.
Cel mai simplu poliedrele Arhimede obținute din poliedre regulate operațiune „TRUNCATE“, constând în tăierea colțuri ale planurilor de poliedru. Astfel, în cazul în care unghiurile de tăiere ale avionului tetraedru, fiecare dintre care taie o a treia porțiune din marginile sale dintr-un nod, obținem tetraedru trunchiat. având opt laturi (Fig.1). Patru dintre ei - hexagoane regulate și patru - triunghiuri echilaterale. La fiecare vârf al poliedrului converg trei fețe.
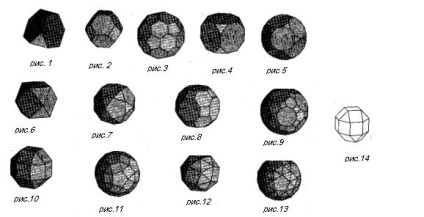
În cazul în care, astfel, tăiate la vârf al octaedru și icosaedru, atunci vom obține, respectiv, un octaedru trunchiată (Figura 2) și un icosaedru trunchiat (Figura 3). Notă. că suprafața suprafeței minge de fotbal se face sub forma unui icosahedron trunchiat. Cubului și dodecaedrul poate obține, de asemenea, cub trunchiată (Figura 4) și dodecaedrul trunchiată (Figura 5).
Pentru a obține un alt poliedru regulat, țineți planul cub de tăiere prin mijlocul marginilor de la un nod. Rezultatul este un poliedru semiregulate, care se numește cuboctahedron (Figura 6). fețele sale sunt șase pătrate ca un cub, și opt triunghiuri echilaterale, la fel ca în octaedru. De aici și numele - cuboctahedron.
În mod similar, în cazul în cală prin punctele de centru marginilor de la un vârf al unui dodecaedru în avioane de interceptare, obținem un poliedru, care se numește icosidodecahedron (Fig.7). El are douăzeci de fețe - triunghiuri regulate și douăsprezece fețe - pentagoane regulate, adică toate fețele de icosaedru și dodecaedrul.
Alte două poliedre sunt numite cuboctahedron trunchiate (Figura 8) și un icosidodecahedron trunchiată (Figura 9), cu toate că ei nu pot obține cuboctahedral trunchierea și icosidodecahedron. ipostazele acestor poliedre de tăiere nu dă pătrate și dreptunghiuri.
Am examinat 9 din 13 descrise de Arhimede poliedre semiregulate. Restul de patru - poliedre de un tip mai complex.
În figura 10 vedem rombokubooktaedr. Suprafața sa constă dintr-un cub și octaedru fețe, la care se adaugă încă 12 pătrate.
Figura 11 descrie rhombicosidodecahedron a cărei suprafață este compusă din fețele icosaedru și un dodecaedru încă 30 de pătrate. Figurile 12, 13 arată (pug) cubului asa-numitul simous și simous (pug) dodecaedrul ale căror suprafețe sunt compuse din cuburi sau dodecaedrul înconjurat triunghiuri regulate.
Pe lângă aceste treisprezece organisme numărul de Arhimede poliedre semi a inclus 14 poliedru numit psevdoarhimedovym (fig.14). Acesta este derivat din rombokubooktaedra cotitură partea de jos a vasului pentru a 45º.
Desigur, în determinarea poliedru semiregulate ECLI slăbi a doua condiție, este posibil să se găsească alte poliedre satisfac această definiție. Cel puțin, există cinci poliedre obținute prin părțile rotative.
Deci, dacă rotiți platanul inferior sau superior icosidodecahedron 36 °, vom obține o nouă poliedru, fețele care sunt pentagoane regulate și triunghiuri converg și patru coaste în fiecare sus.
Strunjire boluri rhombicosidodecahedron pot obține patru mai multe poliedru ale căror fețe sunt pentagoane regulate și pătrate și triunghiuri, și converge cele patru margini la fiecare nod.
Care este definiția unui poliedru semiregulate corect? Care este definiția însemna Archidamus, care a descris treisprezece poliedre semiregulate? Știa el despre corpul psevdoarhimedovom sau nu cred că este posibil de a transforma cuboctahedral castron? Din păcate, definiția poliedre semiregulate, care a fost folosit de Arhimede, să nu se coboare la noi. Aparent, Arhimede nu a considerat psevdoarhimedov poliedru poliedrelor semiregulate.
Într-adevăr, poliedrului aspectul psevdoarhimedov nu este un „drept“ ca poliedre lui Arhimede. Dar ce determină „corectitudinea“?
Reprezentați poliedru semiregulate realizat dintr-un material transparent, si uita-te printr-o singură față n-cărbune. Vom vedea alte fețe, aranjate într-o anumită ordine. Aceeași imagine putem vedea dacă ne uităm printr-o altă față-n GONAL acestei poliedru. Această proprietate este posedat toate poliedre semi-regulat, și poliedru psevdoarhimedov - nr. Dacă te uiți prin partea de sus a unei fata patrata si o fata patrata prin lateral, vedem un aranjament diferit al fețelor rămase.
Din punct de vedere matematic este corectă este determinată de prezența simetrii, adică mișcări care transportă un poliedru la sine.
Arhimede pentru corpurile următoarele proprietăți: pentru oricare două noduri există există o simetrie în care un nod se muta la alta. Acest lucru înseamnă că nu numai toate unghiurile poliedrice de aceeași, dar că, pentru oricare două unghiuri poliedrice ale poliedru există o mișcare care ia una la alta. Desigur, aceasta este o condiție mai puternică decât unghiuri doar egalitate poliedrică. Această condiție nu este îndeplinită poliedru psevdoarhimedov.
Astfel, există trei opțiuni pentru determinarea poliedru semiregulate.
1. Definiția poliedre semiregulate numit un poliedru convex, a cărei suprafață este formată din poligoane regulate - probabil cu un număr diferit de laturi - și la fiecare nod același număr de nervuri. În acest caz, în plus față de cele două serii infinite de prisme și antiprisms, există cel puțin 19 astfel de poliedre.
Definiție 2. poliedru semiregulate numit poliedrului convexă, a cărei suprafață este formată din poligoane regulate - probabil cu un număr diferit de laturi - și toate aceste unghiuri poliedrice sunt egale. În acest caz, în plus față de cele două serii infinite de prisme și antiprisms, există 14 astfel de poliedre - 13 organisme și psevdoarhimedov Arhimede poliedru.
3. Determinarea poliedre semiregulate numit un poliedru convex, a cărei suprafață este format din poligoane regulate - probabil cu un număr diferit de laturi - și pentru oricare două noduri există o simetrie a poliedrului care transformă una în alta. În acest caz, în plus față de cele două serii infinite, există 13 astfel de poliedre - poliedre Arhimede.
Putem presupune că Arhimede a folosit pentru a treia definiție. [9]