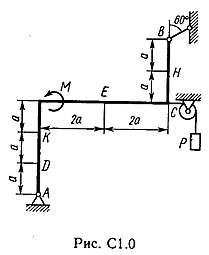
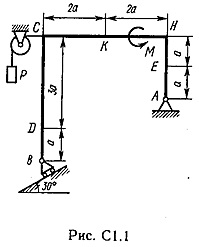
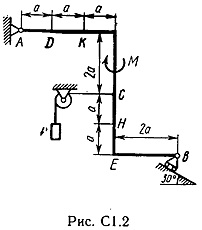
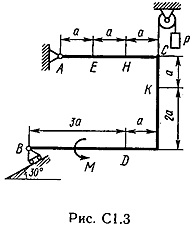
Un cadru rigid este situat într-un plan vertical (figura 1.0 C - .. C 1.9, tabelul C 1) este fixat pivotant la punctul A și un punct atașat sau tijă imponderabil articulată la capete, la suportul balamalei sau pe role.
La punctul C al cadrului de sârmă este atașat, se întinde blocul și purtând la capătul încărcăturii vesomR = 25 kN. Pe rama sunt forțe cuplu din momentomM kNm = 100 și două valori de putere, direcția și punctul de aplicare sunt indicate în tabel.
Se determină reacțiile constrângere, la punctele A, B, cauzate de sarcina. Când calculele finale presupunem a = 0,5 m.
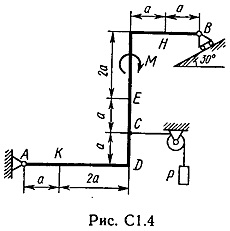
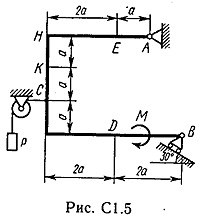
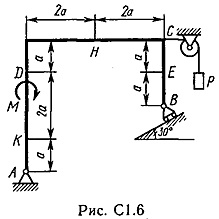
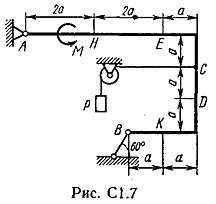
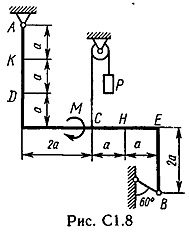
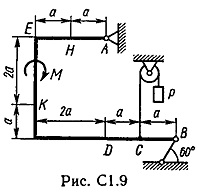
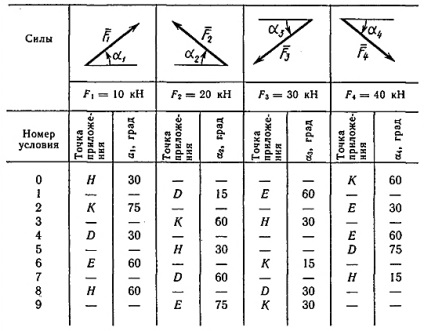
Placă rigidă tochkeA ABCD are un pivot de lagăr fix și un punct de pivot pe role în mișcare.
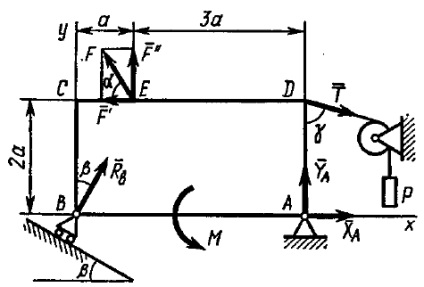
Definiți: reacția la punctele A și B.
1. Să luăm în considerare echilibrul plăcii. Înlocuiți reacțiile de conectare corespunzătoare: cablu de tensiune T (pentru P = modulyuT); balama fix oporuA două componente ha, YA ,; pivotabil-mobile -Rb suport.
2. Pentru un sistem de plan arbitrar al forțelor va fi de trei ecuații de echilibru.
;
;
Substituind în ecuația creată, valorile numerice stabilite valori și rezolvarea acestor ecuații, definim reacția dorită:
După ce a constatat link-urile trebuie să validați reacții cu diferite ecuații de echilibru. De exemplu, pentru a determina suma momentelor tuturor forțelor cu privire la punctul C. Dacă egalitatea va fi egală cu zero, valorile constatat reacțiile identificate corect.
.
2. Determinarea problemă cu reacții de constrângere structură din materiale compozite
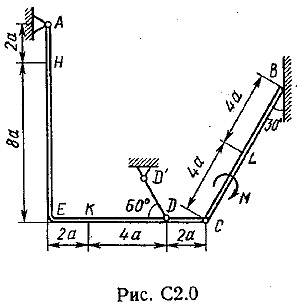
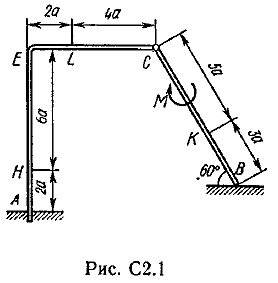
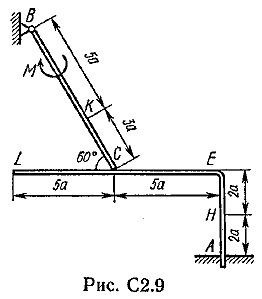
Design-ul este alcătuit dintr-un rigid (Figura C 2.0. - C 2.5) Square și tija, care, la punctul sau conectate între ele sprijinite pivotantă sau liber unul împotriva celuilalt (Figura C 2.6. - 2.9 C). constrângerile externe impuse asupra structurii, sunt în tochkeA sau balama, sau de ancorare; La punctul neted sau plan (1 0 fig.) Sau sterzhenVV imponderabil „(figurile 2 și 3.), sau balamalei (Figura 4-9.); în tochkeD sau sterzhenDD imponderabil „(Fig. 0, 3, 8) sau suportul de articulație pe role (Fig. 7).
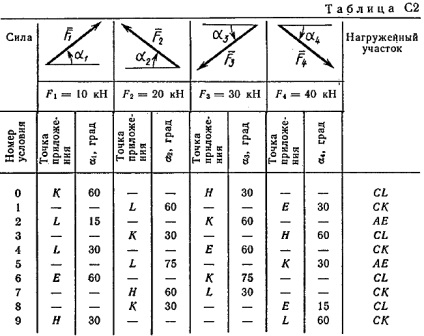
In fiecare desen sunt: o pereche de forțe cu momentul M = 60 kNm uniform distribuite de sarcină intensivnostiq = 20 kN / m și două direcția forței suplimentare și punctele lor de aplicare sunt enumerate în tabelul. C 2; coloană ibidem „porțiune Loaded“, a declarat în ceea ce site-ul funcționează distribuite de încărcare (de exemplu, în condiții № 1 de proiectare sunt silaF2 un unghi de 60 ° față de axa orizontală aplicată în tochkeL, silaF4 un unghi de 30 ° față de axa orizontală, atașată punct, iar sarcina este distribuită pe uchastkeSK).
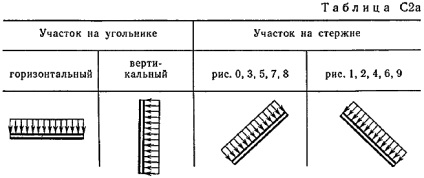
Se determină reacțiile de constrângere la punctele A, B, C (din fig. 0, 3, 7, 8 și chiar în tochkeD) cauzate de sarcină specificată. Când calculele finale, să ia o direcție de sarcină = 0,2 m. Distribuit la diferite site-uri pe locul indicat în tabel. C 2a.
2. grunduri ugolnikABC (AVS = 90 °), al cărui capăt este fixat rigid în tochkeS sterzhenDE se sprijină (Fig. 2 C, a). tijă TochkeD are un lagăr de pivotare și la acesta este atașat fix silaF și gon - uniform sarcină distribuită pe uchastkeKB intensivnostiq și momentomM abur.
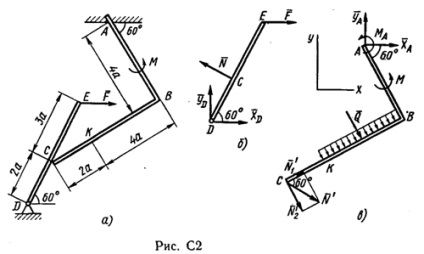
Dată de: F = 10 kN kNm M = 5, q = 20 kN / m, a = 0,2 m Definire :. reacție TochkahA, C, D, din cauza o sarcină predeterminată.
1. Pentru a determina sistemul de reacție și Explode în considerare mai întâi tijă echilibru DE (Fig. 2 C, b). Egal coordonate osiHY și descrie forțele care acționează asupra tijei: siluF, reaktsiyuN îndreptate perpendicular pe tija, și reacția sostavlyayuschieXD iYD sharniraD. Pentru a obține un sistem de forțe plat este de trei ecuații de echilibru:
;
;
.
2. Se consideră echilibrul poligonului (Fig. 2 C, c). Pe ea sunt forța sterzhnyaN de presiune“, în regia opus reaktsiiN, sarcinii uniform distribuite, care înlocuiește siloyQ. aplicat în mijlocul uchastkaKB (chislennoQ = q · 4a = 16 kN), o pereche de forțe și sigiliu strâns momentomM reacție, este compus din forțele care reprezintă sostavlyayuschimiHA, YA si cupluri cu momentomMA. Pentru acest sistem de forțe plat, de asemenea, suntem trei ecuații de echilibru:
;
;
.
În calculul momentului forței N „l-am descompune în sostavlyayuschieN / 1 și N / 2 și se aplică Teorema Pierre Varignon. Substituind în ecuația creată prin valori numerice valori date și rezolvând sistemul de ecuații, obținem reacția dorită. Atunci când deciziile țin cont de faptul că chislennoN „= N, având în vedere egalitatea de acțiune și de reacție.