impulsuri radio (Figura 12) sunt utilizate în practică, frecvența care variază liniar:
în cazul în care - deviația de frecvență, - durata impulsului. Frecvența variază de otdo. semnal de modulație de fază
Perioada medie de frecvență de oscilație. Numărul periodovTo la lungime

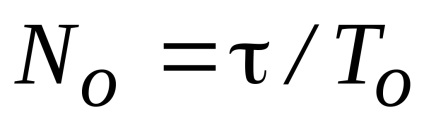
Parametrul principal al semnalului ciripit este în baza sa, care este egală cu produsul din Fig.12. Ciripit semnal dlitelnostina deviatsiyuf 3:
Spectrul oscilațiilor (Figura 13) este destul de complicată. Aceasta este exprimată prin funcțiile speciale - integralele Fresnel. Datorită faptului că în conformitate cu (48), faza (t) este o funcție chiar, toate componentele spectrului au o distribuție uniformă aproximativ chastotyo (tabelul 1, versiunea 1.2).
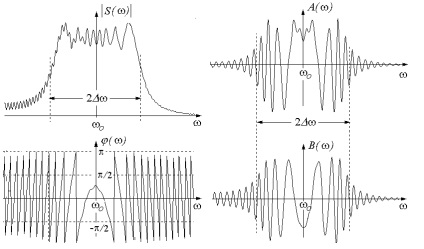
Figura 13. Spectrul cu semnalul ciripit de bază B = 15 și
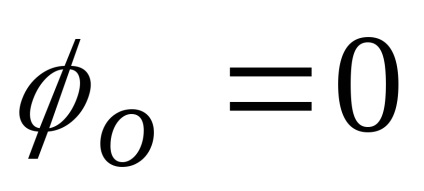
Modulul S () po ca o formă trapezoidală având o lățime la jumătatea înălțimii egale 2. și pante mai abrupte decât baza mare. Spectrul de fază este descrisă de formula
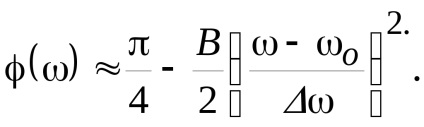
Semnalele ciripit sunt utilizate pe scară largă în sistemele de radar optime distanță de recepție, și, prin urmare, joacă un rol important al funcției de autocorelare, plicul a cărui formă este aproape de o funcție (fig.14) 4. cu o lățime lob
În lățimea lobului centrale 2t ukladyvaetsyaN periodovTo oscilații de frecvență purtătoare:
Dacă 1 >> Lobul centrală are un vârf de corelație îngustă. Raportul este denumit raportul de compresie.
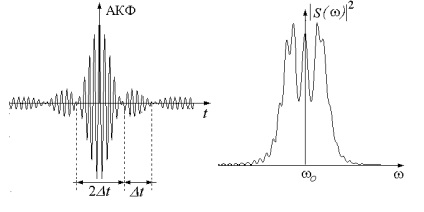
Figura 14. Funcția de autocorelație a semnalului ciripit (a) și spectrul său (b)
2.4. Amplitude unghi de modulare (Aum)
Când AUM conform (1) și (2), semnalul poate fi reprezentat ca
Dacă funcția F (t) este periodică cu periodomT = 2. ea poate fi reprezentată prin seria Fourier cu frecvențe complexe amplitudamiFn:
Această înregistrare poate fi interpretată ca o sumă de armonici
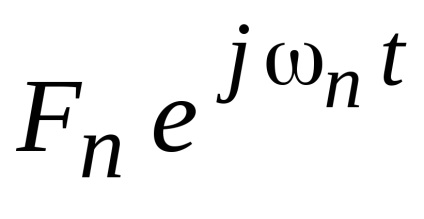
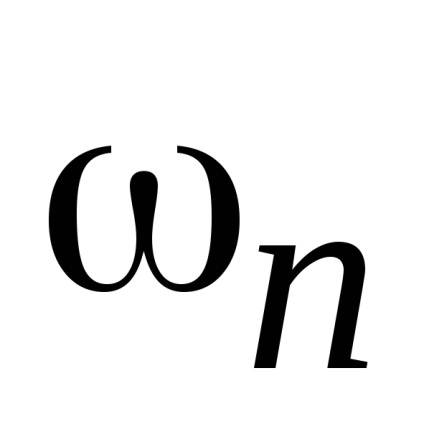
În cazul în care cu aceeași perioadă T, calendarul și amplitudinea, atunci acesta poate fi reprezentat prin seria Fourier cu amplitudamiUm complexă:
are o armonici de frecvență parțială rezultă a spectrului. Numărul lor este
Vezi spectrului de frecvențe este destul de complex. cazuri particulare când variază simetria funcțiilor U (t) i (t) este descris în tabelul 1. semnal cu EXEMPLU periodic funktsiyamiU (t) i (t) este prezentat în Fig.15.
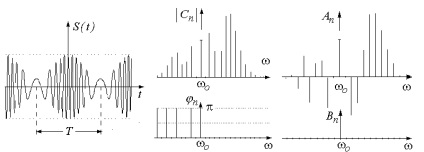
Figura 15. semnal Aum (a) și spectrele sale (b, c) pentru
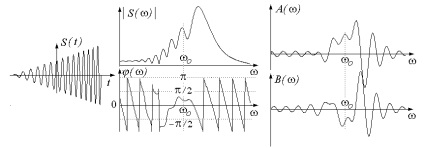
Figura 16. semnal unic Aum cu AM sawtooth
și FM liniar cu bază = 5
În unele cazuri, este posibil să se facă o evaluare comparabilă a semnalului și spectrul său. De exemplu, din figura 16 se observă că modulul crește densitatea spectrală aproape liniar cu frecvența în creștere, ceea ce corespunde unei creșteri a curentului amplitudinea semnalului de oscilație cu durata perioadei curente în scădere.