mișcare corp rigid în care O și O două puncte „sunt fixe, numită o mișcare de rotație în jurul unei axe fixe și o linie dreaptă fixă DD“ se numește axa de rotație.
Lăsați un corp rigid rotativ în jurul unei axe fixe OO „(fig. 2.12).
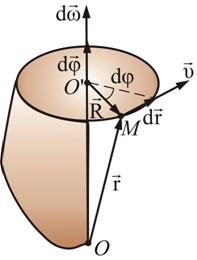
Trace pentru un punct M al corpului rigid. În timpul dt punctul M face dr deplasare elementară.
Dacă același unghi de rotație d cp, un alt punct, a cărui distanță față de axa la o distanță mai mare sau mai mică, face o altă mișcare. În consecință, nici deplasarea punctului unui corp solid, sau primul derivat sau derivat al doilea poate servi ca o caracteristică a mișcării nu numai solid.
În timpul acestui vector aceeași rază de timp dt trasată de la punctul 0 „la punctul M. rândul său printr-un unghi d φ. În același unghi rotire a vectorului rază de oricare alt punct (ca organismul este absolut rigid, altfel distanța dintre punctele care trebuie schimbate).
Unghiul de rotație d φ caracterizează mișcarea întregului corp în timpul timpul dt.
Convenabil intra - vector de rotație elementară a corpului, care este numeric egal cu d φ este direcționată de-a lungul axei de OO rotație“, astfel încât, în căutarea de-a lungul vectorului, am văzut o rotire în sens orar (direcția vectorului și direcția de rotație a«regula de degetul mare»asociat).
Rotațiile elementare satisface regula obișnuită de adăugare vector:
Este viteza unghiulară vectorul este numeric egal cu primul derivat al unghiului de rotație în timp și direcționată de-a lungul direcției axei de rotație (și întotdeauna în aceeași direcție).
Dacă ω - Const, atunci există o rotație uniformă a corpului în jurul unei axe fixe.
Fie v - viteza lineară a punctului M. În timp punct intervalul dt M merge mult dr = vdt. În același timp dr = Rd φ (dφ - unghi central). Apoi, puteți obține o viteză legătură liniară și unghiulară:
În formă vectorială.
Vector este ortogonal vectorilor și și îndreptat în aceeași direcție ca și produsul vectorial.
Odata cu perioada de viteză unghiulară de rotație și utilizează conceptul de frecvență de rotație.
PeriodT - un interval de timp în care organismul face o rotație completă (adică rotație cu un unghi φ = 2π).
VA de frecvență - numărul de rotații ale corpului în 1 secundă.
Atunci când se rotește cu viteza unghiulară ω, avem:
Noi introducem vectorul accelerației unghiulare a caracteristicilor de rotație neuniformă a corpului:
Vector este îndreptat în aceeași direcție ca și cea de rotație a accelerat și îndreptat în direcția opusă de rotație lentă (fig. 2.13).
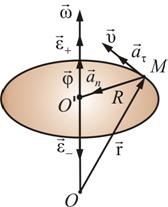
Ca orice punct de organism firmă, punctul M este componentele normale și tangențiale de accelerație. Ne exprimăm normal și tangent la punctul de accelerare M a vitezei unghiulare și accelerația unghiulară: