5.1. concepte de bază
Valorile sunt complet determinate prin valoarea lor numerică, numită scalar. Exemple de cantități scalare sunt: suprafață, lungime, volum, temperatură, masa de lucru.
Alte valori, cum ar fi puterea, viteza, accelerația, sunt determinate nu numai prin valoarea sa numerică, dar și direcția. Aceste valori sunt numite vector. Geometric reprezentat de o mărime vectorială cu un vector.
Vector - un segment de linie îndreptate, adică segmentul având o anumită lungime și o anumită direcție ... Dacă A - începutul vectorului și B - sfârșitul acesteia, atunci vectorul este desemnat ca AB sau simbol. Vector BA (el care pornește de la punctul B și se termină la punctul A) se numește un vector opus AB. Vector și vectorul opus. Înseamnă - o.
Lungimea sau un modul al vectorului AB este numit lungimea segmentului și este notat cu | AB |. Lungimea vectorului este egal cu zero se numește vectorul zero și este notat cu 0. direcția de vector zero, nu contează.
Vector a cărui lungime este egală cu unul este numit un vector unitate și este notat cu e. Versorul a cărei direcție coincide cu direcția vectorului a. Este numit un vector unitate al vectorului și este notat cu o °.
Vectori a și b se numesc coliniari dacă se află pe aceeași linie sau linii paralele; înregistrarea unui || b.
vectori coliniari pot fi aceleași sau orientate opus.
Zero vector este considerat a fi orice vector coliniare.
Două vector a și b sunt numite egale (a = b), în cazul în care sunt coliniari, aceeași direcție și au aceeași lungime.
Din definiția egalității vectorilor că vectorul poate fi deplasat paralel cu ea însăși, și începutul Vector plasat în orice punct al spațiului.
In Figura 1, vectorii formează un dreptunghi. Egalitatea pe b = d. dar cu un ¹. Vectorii o și - dimpotrivă, a = - p.
Vectorii Egale sunt denumite liber.
Trei spațiu vectorial sunt numite coplanare. dacă se află în același plan sau în planuri paralele. Dacă printre cei trei vectori cel puțin un zero sau două toate coliniare, astfel de vectori sunt coplanari
5.2. operațiuni liniare cu vectori
În cadrul operațiunilor liniare cu vectori înțeleg operațiile de adunare și scădere a vectorilor și înmulțirea vectorului de un număr.
Fie a și b - doi vectori arbitrare. Ia-un punct arbitrar O și construi un vector OA = o. Din punctul A vector decaleze AB = b. Vector OB. conectarea la începutul primului vector cu al doilea capăt, numit suma vectorilor a și b. O B = a + b (a se vedea. Fig. 2)
.
Această regulă se numește regula de triunghi plus vectorului. Suma a doi vectori pot fi, de asemenea, construite conform regulii de paralele; o grame (vezi. Fig. 3).
Figura 4 prezintă adăugarea a trei vectori, precum și. b și c.
Sub vectorii de diferență și vectorul b și c medie = a - b astfel încât b + c = a (a se vedea figura 5 ..).
Rețineți că în paralelogramului construit pe vectorii a și b, una de-a lungul diagonalelor este suma vectorilor a și b, iar celălalt - diferența (a se vedea figura 6 ..).
Este posibil să se scadă vectori conform regulii: a - b = a + (- b), adică scăderea adăugarea vectorilor vectorului și înlocuit cu un vector opus la vectorul b ...
Produsul vectorului și un scalar (întreg) # 955; Este un vector # 955; * A (sau A * # 955;), care are o lungime | # 955; | * | și |, este coliniare cu un. și are un vector de direcție. dacă # 955> 0, iar în direcția opusă, dacă # 955;<0. Из определения произведения вектора на число следуют свойства этого произведения:
1) în cazul în care b = # 955; * A. apoi b || a. Pe de altă parte, în cazul în care b || a. (A ¹ 0), atunci pentru unele # 955; egalitatea b = # 955; și;
2) este întotdeauna o = | și | • și -O. t. e., fiecare vector este egal cu produsul dintre modulul său în vectorul unitate.
operații liniare cu vectori au următoarele proprietăți:
1. a + b = b + a
2. (a + b) + c = a + (b + c),
3. # 955; 1 • (# 955; 2 • a) = # 955; # 955 1 • 2 • și,
4. (# 955, # 955 + 1; 2) • a = # 955; a + 1 • # 955; 2 • și,
5. # 955; • (a + b) = # 955; • un + # 955; • b.
Aceste proprietăți permit conversia operațiunilor vectoriale liniare așa cum se face în algebra obișnuită: termenii interschimbate, sar peste paranteze la grup, pentru a face consolele ambelor scalare și vectoriale factori comuni.
5.3. Proiecția vectorului pe axa
In spatiul definit axa l, t. Linia E. Directed.
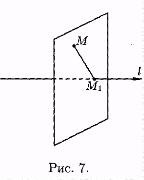
Punctul de proiecție M pe axa l numește bază M1 perpendicular MM1. a scăzut de la un punct de pe axa.
punctul M1 este punctul de intersecție al axei l cu planul care trece prin punctul perpendicular pe axa M (vezi. fig. 7).
Dacă M se află pe axa l. proiecția punctului M pe axa coincide cu M1.
Să AB - vector arbitrar (AB ¹ 0). Notăm A1 și 1 b a proiecției pe axa l respectiv încep A și vectorii final B AB și ia în considerare vectorul A 1 B 1
Proiecția vectorului AB pe axa L este declarat a fi un număr pozitiv | A 1 B 1 |. axa dacă vectorul A 1 l 1 și sunt direcționate în mod similar și numărul de negativ - | A 1 B 1 |. dacă vectorul A axa 1 B 1 și l în direcții opuse (vezi. fig. 8). Dacă punctele de b 1 1 și sunt aceleași (A 1 B 1 = 0), atunci proiecția vectorului AB este 0.
Proiecția vectorului AB la axa l pr l notate AB. Dacă AB = 0 sau AB ^ l. PRL AB = 0.
Unghiul j între vectorul a și axa l (sau unghiul dintre doi vectori) este prezentată în Figura 9. Evident, 0 £ j £ p
Să luăm în considerare câteva dintre proprietățile de bază ale proiecțiilor.
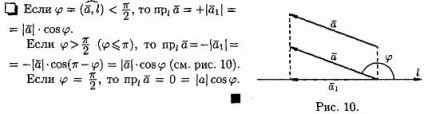
Proprietatea 1. Proiecția unui vector pe axa l este egală cu produsul unui vector unitate pe cosinusul unghiului j între vectorul și axa, adică, un l drept = .. | o | • cos j.
Corolarul 5.1. Proiecția vectorului pe axa pozitivă (negativă) dacă vectorul formează un unghi ascuțit (obtuz) a axei, și este zero, atunci când unghiul de - line.
Corolarul 5.2. Vectorii de proiecție egale cu una și aceeași axă sunt egale.
Proprietatea 2. Proiecția suma mai multor vectori pe aceeași axă este egală cu suma proiecțiilor lor pe această axă
Proprietatea 3. Când multiplicarea vectorului și numărul A al proiecției sale pe axa este, de asemenea, înmulțită cu numărul m. E.

Astfel, operațiile liniare cu vectori rezultat operații corespunzătoare pe proiecții liniare ale acestor vectori.
5.4. Descompunerea vectorului unitar vectorii axelor de coordonate.
modul vector. cosinusului direcție.
În dreptunghiular spațiu Oxyz sistem de coordonate. Selectăm pe axele de coordonate Ox, Oy și vectori unitate Oz (vectori de bază), se face referire la i. j. k, respectiv (vezi. fig. 12).
Alegeți un vector arbitrar un spațiu și este compatibil cu origine superioară: a = OM.
Noi găsim proiecția vectorului și axele de coordonate. Prin capătul planului OM vectorului paralel cu coordonate plane. Punctele de intersecție ale acestor avioane cu axe notate cu M 1 și M2 Mz.Poluchim paralelipipedică, din care una este diagonală OM vector. Etc Apoi, x = o | OM 1 |, NPY a = | OM 2 |, etc și z = | OM s |. Prin definiție, suma mai multor vectori găsi = 1 OM + M1 N + NM.
Deoarece M 1 N = OM 2. NM = OM s, atunci
Notăm proiecția vectorului a = OM pe Ox, Oy și Oz respectiv prin ah. ay și az. și anume | OM 1 | = Ax, | OM 2 | = Ay. | OM 3 | = A z. Apoi, rezultă din (5.1) și (5.2)
Această formulă este vectorul principal și calculul se numește un vector de descompunere a unit vectorii axelor de coordonate. Numărul de ah. ay. Coordonatele az sunt numite vector a, t. e. coordonatele proiecției sale este pe axa de coordonate corespunzătoare.
Ecuația vectorială (5.3) este adesea scris într-o formă simbolică: a = (ax; ay, az).
Ecuația b = (bx; prin; bz) înseamnă că b = b x • i + b y • j + bz • k. Cunoașterea componentelor vectorului a. puteți găsi cu ușurință expresia unității vectorului. Pe baza teoremei asupra lungimii diagonalei unui paralelipiped poate scrie
t. e. egal cu mărimea rădăcinii pătrate a sumei pătratelor proiecțiile pe axele.
Lăsați un unghi vector cu axele Ox, Oy și Oz sunt, respectiv a, b, g. Prin proprietatea proiecția axei, avem
Sau ce este același lucru,
Numerele sunt numite cosinus direcția vectorului a.
Înlocuim expresia (5.5) în (5.4), obținem
Reducerea pentru a obține relația
t. e. suma pătratelor direcția cosinusului vectorul nenul este egal cu unu.
Este ușor de observat că coordonatele vectorului unitate e sunt numere
Astfel, prin stabilirea coordonatelor vectorului este întotdeauna posibil să se determine magnitudinea și direcția sa, și anume, vector în sine.