Definiția 1. dreptunghi - o figură geometrică plană formată din patru puncte, linii conectate astfel încât acestea să nu se intersectează nicăieri, cu excepția chiar în aceste puncte.
Definiție 2. dreptunghi - un dreptunghi în care două laturi opuse sunt egale și toate cele patru colțuri sunt aceleași.
Dreptunghi poate fi un paralelogram, un pătrat sau un romb. Prin urmare, este posibil să se formuleze definiția unui dreptunghi.
Definiția 3. dreptunghi - un paralelogram care are toate cele patru colțuri sunt drepte.
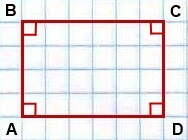
Latura lungă a dreptunghiului se numește lungimea dreptunghiului, și scurt - lățimea dreptunghiului.
Ambele părți ale dreptunghiului este înălțimea sa.
Principalele proprietăți ale dreptunghiului
1. Laturile opuse ale dreptunghiului sunt de aceeași lungime, adică, acestea sunt:
2. Partea opusă a dreptunghiului paralel:
3. Laturile adiacente ale dreptunghiului sunt întotdeauna perpendiculare:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Toate cele patru colțuri ale liniilor de dreptunghi:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90 °
5. Colțurile dreptunghiului este egal cu suma de 360 de grade:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360 °
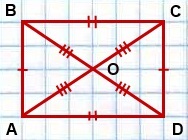
7. Suma pătratelor diagonalei dreptunghiului este egal cu suma pătratelor laturilor:
2 = 2d 2a + 2b 2 2
8. Fiecare dreptunghi diagonală împarte dreptunghi în două părți egale, și anume, triunghiuri in unghi drept.
9. dreptunghi diagonalele se intersectează în punctul de intersecție împărțită în jumătate:
AO = BO = CO = DO = d / 2
10. Punctul de intersecție al diagonalelor dreptunghiului se numește un centru și, de asemenea, centrul circumscris
11. Dimensiunea dreptunghiului este diametrul cercului circumscris
Lungimea dreptunghiului se numește lungimea perechii mai lungă de laturi.
Lățimea dreptunghiului este numită lungimea perechii mai scurtă dintre laturile sale.
De multe ori problemele necesare pentru a găsi lungimea dreptunghiului, mai jos furnizează formule pentru această
Formula determina lungimile laterale ale dreptunghiului
1. Formula de dreptunghi (lungimea și lățimea dreptunghiului) printr-o diagonală și cealaltă parte:
a = √ (d 2 - b 2) și, respectiv, b = √ (d 2 - a 2)
Dovada: Proprietate 2 7. 2d = 2a + 2b 2 2 # 8658 (timp pentru detalii scurta 2) d 2 = a 2 + b 2 # 8658 a 2 = d 2 - b 2 # 8658 a = √ (d 2 - b 2)
2. Formula dreptunghiului (lungime dreptunghi și lățime) peste pătrat și cealaltă parte:
a = S / b, respectiv, și b = S / a
Dovada: S = a • b # 8658 a = S / b sau b = S / a
3. Formula de dreptunghi (lungimea și lățimea dreptunghiului) și prin perimetrul cealaltă parte:
a = (P - 2b) / 2, respectiv, și b = (P - 2a) / 2
Dovada: P = 2 (a + b) # 2 8658 b = (P - 2a) # 8658 b = (P - 2a) / 2
4. Formula dreptunghiului (lungime dreptunghi și lățime) a diametrului și a unghiului a:
a = d sinα și în consecință b = d cosα
5. Formula dreptunghiului (lungime dreptunghi și lățime) a diametrului și unghiul p:
a = d păcat β / 2 și, respectiv, b = cos d p / 2
Diagonala unui dreptunghi este orice segment care leagă două vârfuri ale colțuri opuse ale unui dreptunghi.
Formula determina lungimea diagonalei unui dreptunghi
1. Formula dreptunghi în diagonală pe cele două laturi ale dreptunghiului (teorema lui Pitagora):
Dovada: Suma pătratelor diagonalei dreptunghiului este egal cu suma pătratelor laturilor:
2 = 2d 2a + 2b 2 2
2. Formula dreptunghiului în diagonală peste pătrat, și nici un fel:
d = (√ (S 2 + 4)) / a = (√ (S 2 4 + b)) / b
3. Formula dreptunghi în diagonală pe perimetrul și orice direcție:
d = (√ (P 2 - 4Pa + 8a 2)) / 2 = (√ (P 2 - 4PB + 8b 2)) / 2
4. Formula dreptunghi diagonală pe raza cercului circumscris:
5. Formula diagonal prin dreptunghi circumscris diametrul cercului:
6. Formula dreptunghi în diagonală peste sinusul unghiului adiacent diagonală, iar lungimea laturii opuse unghiului:
7. Formula dreptunghi în diagonală prin cosinusul unghiului adiacent la lungimea diagonalei laturii și adiacente acestui colț:
8. Formula diagonală prin dreptunghiului unghi ascuțit sinusoidală între diagonalele dreptunghiului și zona
Perimetrul unui dreptunghi este suma lungimilor tuturor laturile dreptunghiului.
Formula determina lungimea perimetrului unui dreptunghi
1. Formula perimetrului unui dreptunghi două laturi ale dreptunghiului:
P = 2a + 2b sau P = 2 (a + b)
Onlyayn calcula perimetrul aici
2. Formula perimetrului unui dreptunghi peste zona si fiecare parte:
P = (2S + 2a 2) / a = (2S + 2b 2) / b
3. Formula perimetrului unui dreptunghi peste diagonală și nici un fel:
P = 2 (a + √ (d 2 - a 2)) = 2 (b + √ (d 2 - b 2))
4. Formula perimetru dreptunghiular al raza cercului circumscris și orice direcție:
P = 2 (a + √ (4R 2 - a 2)) = 2 (b + √ (4R 2 - b 2))
5. Formula perimetru dreptunghiular din diametrul cercului circumscris și orice direcție:
P = 2 (a + √ (Do 2 - a 2)) = 2 (b + √ (Do 2 - b 2))
Zona dreptunghiului este spațiul delimitat laturile dreptunghiului, adică, în perimetrul dreptunghiului.
Formulele pentru determinarea suprafeței unui dreptunghi
1. Zona de Formula dreptunghiului în două aspecte:
Calculeaza online aria unui dreptunghi poate fi aici
2. Formula zona dreptunghiului prin perimetrul și orice direcție:
S = (Pa - 2a 2) / 2 = (Pb - 2b 2) / 2
3. Formula zona dreptunghiului prin cale diagonală și fie:
S = a√ (d 2 - a 2) = b√ (d 2 - b 2)
4. Formula dreptunghi prin pătrat diagonală și a sinusurilor unghi ascuțit între diagonalele:
5. Zona de Formula dreptunghiului descris de raza cercului și orice direcție:
S = a√ (4R 2 - a 2) = b√ (4R 2 - b 2)
6. Formula zona dreptunghiului diametrului cercului circumscris și orice direcție:
S = a√ (Do 2 - a 2) = b√ (Do 2 - b 2)
Cercul descris în jurul dreptunghiului
Cercul descris în jurul dreptunghiului este numit un cerc care trece prin cele patru noduri ale unui dreptunghi al cărui centru se află la intersecția diagonalelor dreptunghiului.
Formulele pentru determinarea dreptunghiului raza cercului circumscris
1. Formula raza cercului circumscris dreptunghi cu două laturi:
2. Formula razei cercului circumscriere dreptunghi și prin perimetrul unui pătrat orice direcție:
R = (√ (P 2 - 4Pa + 8a 2)) / 4 = (√ (P 2 - 4PB + 8b 2)) / 4
3. Formula raza cercului circumscris dreptunghi printr-o zonă de pătrat:
R = (√9S 2 + 4)) / 2a = (√ (S 2 + b 4)) / 2b
4. Formula raza cercului circumscris dreptunghi prin diagonala pătrat:
5. Formula raza cercului circumscris dreptunghi din diametrul cercului circumscris:
6. Formula raza cercului în jurul dreptunghiului descris de sinusul unghiului adiacent diagonală și lungimea opusă acestui unghi:
7. Formula raza cercului circumscris dreptunghi de cosinusul unghiului adiacent la lungimea diagonalei laturii și adiacente acestui colț:
8. Formula raza cercului circumscris dreptunghi sinusoidal printr-un unghi ascuțit între diagonalele dreptunghiului și aria:
Unghiul dintre laturile și diagonalelor dreptunghiului
Formula determină unghiul dintre laturile și diagonalele
1. Formula determinarea unghiului dintre laturile și diagonalelor dreptunghiului prin diagonală și laterale:
păcatul α = a / d, respectiv și cos α = b / d
2. Formula determinarea unghiului dintre laturile și diagonalelor dreptunghiului cu unghiul dintre diagonalele:
Unghiul dintre diagonalele dreptunghiului
Formula determină unghiul dintre diagonalele dreptunghiului
1. Formula determinarea unghiului dintre diagonalele dreptunghiului de unghiul dintre laturile și diagonalele:
2. Formula determinarea unghiului dintre diagonalele dreptunghiului diagonală peste pătrat și: