Găsirea maximă a funcției obiectiv
Noi folosim modelul construit pentru compania Reddy Mikks, pentru a arăta ambele etape ale soluției grafică a problemei LP.
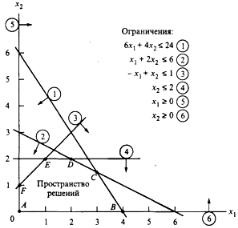
Pasul 1: Construirea unui spațiu de soluții fezabile.
Axa prima extragere sunt indicate pe valoarea orizontală a variabilei x 1 și
pe verticală - x 2. Apoi, ia în considerare starea de non-negativitate de variabile: x 1, x 2 0 și 0. Aceste două constrângeri arată că spațiul de soluții viabile se va afla în primul cadran.
Pentru a ține cont de restricțiile rămase înlocuiesc inegalitatea la egalitate, cu rezultatul că obținem ecuațiile liniilor, iar apoi avionul va organiza aceste linii.
Acum, ia în considerare modul în care grafic interpretate inegalitatea. Fiecare inegalitate împarte planul x 1 x 2 în două jumătăți, care sunt situate pe ambele părți ale liniei care corespunde acestei inegalități. punctul avion
situat pe o parte a liniei drepte satisfaceti (pe jumătate admisibil), iar punctele care se află pe cealaltă parte - nr. Punct „Test“
punctul Verificări de jumătate de satisfaceti, și ceea ce - nu,
poate servi drept punct (0, 0). De exemplu, acest punct satisface o primă inegalitate
X 6 x 1 april 24 februarie (aici 6 * 0 + 4 * 0 = 0 <24 ). Это означает, что точки полупространства,
care conține punctul de pornire (0,0), satisfac această inegalitate. Fig. 1
admise jumătate de săgețile afișate.
În cazul în care punctul (0,0) nu satisface inegalitatea, este permisă halfspace, care nu conține punctul. Dacă linia trece prin acest punct, ar trebui să fie ca un „test“ pentru a lua orice alt punct.
Pasul 2: Găsirea soluției optime.
Punct al spațiului de soluții fezabile, așa cum se arată în Fig. 1, îndeplinesc
în același timp, toate constrângerile. Acest spațiu este delimitat de segmente de linie, care sunt unite la punctele de colț A, B, C, D, E și F. Orice punct situat în interiorul sau pe frontiera regiunii delimitate de ABCDEF poligon, este o soluție fezabilă, adică,
satisface toate constrângerile. Deoarece spațiul de soluții fezabile conține un număr infinit de puncte, necesită o anumită procedură pentru găsirea de soluții optime.
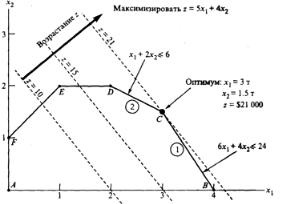
Găsirea soluției optime necesită determinarea direcției creștere a funcției obiectiv z x 5 x 1 2 aprilie putem echivala cu un număr z valori în creștere, cum ar fi 10 și 15. Aceste valori, derivații substituiți în locul z în expresia funcției obiectiv, generează ecuațiile liniilor; pentru 10 și 15 valori ale ecuației obținem directe
5 x 2 x 04 ianuarie 10 si 04 ianuarie x 5 x 2 15. Fig. 2, aceste linii sunt afișate prin linii întrerupte și
direcția de creștere a funcției obiectiv - săgeata mare. Funcția obiectiv poate crește atâta timp cât liniile drepte corespunzătoare importanței tot mai mare a acestei funcții, traversează regiunea de soluții fezabile. Punctul de intersecție al zonei de soluții fezabile și linia corespunzătoare valoarea maximă posibilă a funcției obiectiv,
și va optimul punct.
Fig. 2 arată că soluția optimă corespunde punctului C. Acest punct este un punct de trecere a liniilor (1) și (2), astfel încât coordonatele x 1 și x 2 sunt soluția unui sistem de ecuații care definesc aceste linii:
Soluția acestui sistem este x 1 = 3 și x 2 = 1,5, valoarea valorii funcției obiectiv z = 21. Decizia rezultată înseamnă că, pentru compania Reddy Mikks cea mai bună alegere este o producție zilnică de 3 tone de vopsea pentru exterior și 1,5 tone - pentru interior funcționează cu un venit zilnic de 21.000.