Valorile rândurilor index sunt non-negativ, prin urmare, vom obține soluția optimă:,; .
Raspuns: Profitul maxim din vânzarea de bunuri fabricate, egală cu 160/3 unități. Acesta asigură eliberarea de numai al doilea tip de produse în valoare de 80/9 unități.
Ținta № 2
Dana problemă de programare neliniară. Găsiți maxim și minim al funcției obiectiv al metodei grafice-analitice. Crearea funcției Lagrange și arată că condiții suficiente pentru un minim (maxim) a alerga în punctele extremum.
pentru că ultima cifră a numărului de cod este 8, atunci A = 2; B = 5.
pentru că penultimul număr de cod cifre este de 1, ar trebui să selectați numărul de activitate 1.
1) Desenați o regiune care definește sistemul de inegalități.
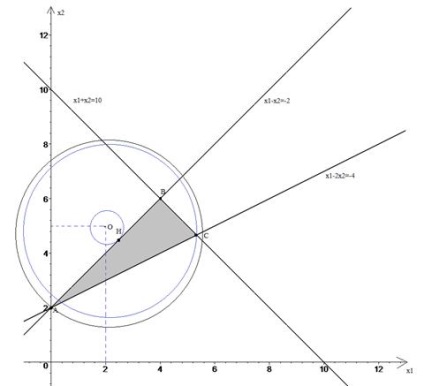
Această zonă - triunghiul ABC cu vârful coordonate: A (0, 2); In (4, 6) și C (16/3; 14/3).
Nivelurile funcției țintă sunt cercuri cu centru la punctul (2, 5). Pătratele razelor vor fi valorile funcției obiectiv. Apoi, pe figură arată că valoarea minimă a funcției obiectiv este obținut la punctul H, maxim - fie prin punctul A sau C.
Valoarea funcției obiectiv la punctul k;
Valoarea funcției obiectiv la punctul C :;
Prin urmare, cea mai mare valoare este obținută la punctul A (0, 2) și este egal cu 13.
Găsim coordonatele punctului N.
Pentru a face acest lucru, considerăm sistemul:
Linia este tangenta la cercul dacă ecuația are o soluție unică. Ecuația pătratic are o soluție unică, în cazul în care discriminant este 0.
apoi; ; - valoarea minimă a funcției.
2) funcția Lagrange pentru găsirea soluției minimă:
condiții suficiente pentru un extremum:
Sistemul are o soluție, adică, Condițiile de optimalitate suficiente sunt îndeplinite.
Funcția Lagrange pentru a găsi rezoluția maximă:
condiții suficiente pentru un extremum:
Sistemul are, de asemenea, o soluție, care este, Condițiile de optimalitate suficiente sunt îndeplinite.
Răspuns: Funcția obiectiv minim este atins prin; ; un maxim al funcției obiectiv este atins atunci când; .
Ținta № 3
Două întreprinderi într-o cantitate de fonduri alocate unităților d. Atunci când alocă prima entitate înseamnă un an de unități x unități pe care le oferă k1x venituri, precum și alocarea a doua unități de y întreprindere înseamnă că furnizează unități de k1y venit. Soldul la sfârșitul anului, pentru prima întreprindere este nx. a doua mea. Cum de a distribui toate fondurile pe parcursul celor 4 ani de la venitul total a fost cel mai mare? Problemă rezolvată prin metoda programării dinamice.
Întreaga perioadă de o durată de 4 ani împărțit în 4 faze, fiecare dintre acestea fiind egală cu un an. Să enumerăm etapele din primul an. Să XK și Yak - fonduri alocate, respectiv, întreprinderilor A și B k - această etapă. Apoi, suma Hk + Yk = ak este suma totală a fondurilor utilizate în k - etapa iar restul din etapa anterioară k - 1. în prima etapă, folosind toate fondurile alocate și a1 = 2200 unități. venitul care este primit pe k - etapa în alocarea unităților XK și Yak va fi 6Hk + 1Yk. lasa venitul maxim primit în ultimele etape începând cu k - etapa este de unități fk (AK). vom scrie ecuația funcțională Bellman, care exprimă principiul optimalității: ce ar fi fost starea inițială și decizia inițială a deciziei ulterioare trebuie să fie optimă în raport cu starea care rezultă din starea inițială:
Pentru fiecare etapă, trebuie să selectați Hk. și valoarea AK- Yk = Xk. În acest sens, vom găsi randamentul k - etapa:
ecuație funcțională Bellman va arata:
Luați în considerare toate etapele, începând cu ultimul.
(Deoarece funcția liniară maximă este atinsă la sfârșitul intervalului [0, a4] când x4 = a4);
(Deoarece funcția liniară maximă este atinsă la sfârșitul intervalului [0; a3] pentru x3 = a3)
(Deoarece funcția liniară maximă este atinsă la sfârșitul intervalului [0, a2] la x2 = a2)
(Deoarece funcția liniară maximă este atinsă la sfârșitul intervalului [0; a1] la x1 = a1). a1 = y1 - x1 = 0.
Astfel, venitul maxim pentru al 4-lea an va fi
R: Banii trebuie investiți numai în companie și veniturile totale pentru anul se va ridica la 16,473.6 4 unități.
Număr Sarcina 4
Determina - gama optimă parametric de produse pentru a satisface cererea prestabilită, și anume numărul de tipuri de produse N, valorile parametrilor (k = 1,2, ..., 5) de produse pentru care costul total reduse, mai multe tipuri de produse, fiecare produs deservită de selectat K-st tip - numărul de articole din fiecare tip necesare pentru a satisface cererea și costul minim al fiecărui produs de tip K-lea:
Construi un arbore de decizie complet și arată modul în care ramurile sale sunt tăiate folosind o ramură și metoda de legat, și ca o consecință, reduce cantitatea de calcule, în comparație cu metoda de completă