Definiție 8. Intervalele în care funcția stochează un anumit semn, numite intervale de semn constant al funcției.
Evident, graficul funcției se află deasupra axei x, și când mai jos, atunci când se schimbă funcția de semn, la trecerea prin zerouri sau punctul de rupere. În intervalul în care funcția este continuă și nu are zerouri, semnul său este salvat.
2.7.1. Algoritmul pentru identificarea intervalelor de conectare constantă
1) Găsiți domeniul funcției
2) Rezolva rădăcinile ecuație, vor fi incluse în zerouri.
3) pe linia de numărul de a pune domeniul funcției și zerouri. În intervalele obținute pentru a determina funcția de conectare.
4) Identificarea intervalelor funcției semn constant.
Exemplul 2.5. Găsiți intervalele ale funcției semn constantă.
1. Domeniul definiției funcției
2. Să ne rezolve ecuația zerourile sunt puncte
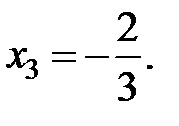
originea (adică. e. o linie la care curba graficului devine arbitrar aproape). Distinge asimptotă verticală, orizontală și oblică. Definiția 14. Noi spunem că linia este asimptota verticală a graficului funcției, dacă (fig. 5).
Teorema Teorema 4. Direct este asimptota oblici grafic funcție (fig. 5), dacă și numai dacă există limite finite
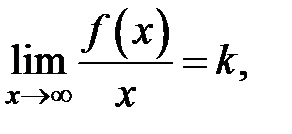
1. Definiția implică faptul că asimptota verticală trebuie să se uite la punctele de discontinuitate a infinitului (în al doilea tip de puncte de pauză). Atunci când se apropie de un punct de discontinuitate (cel puțin pe o parte - la stânga sau la dreapta) tinde la infinit graficul funcției arbitrar aproape de o linie dreaptă
2. Graficul funcției poate avea orice număr de asymptotes verticale sau nu au.
3. Pentru a determina prezența asimptota trebuie luate în considerare separat, în limitele și în legătură cu această funcție poate
- au aceeași înclinat la asimptota (Fig.6 a);
- au diferite asimptota oblică la și (figura 6, b).
-Au asimptotă înclinată numai dacă sau când (fig. 6c).
4. Un caz special al asymptotes înclinate (la) este o asimptotă orizontală. Direct este o asimptotă orizontală a graficului unei funcții, la un moment dat și numai atunci când
5. Funcția Schedule se pot intersecta cu oblică și gorizontalnoyasimptotami un număr finit sau infinit de puncte.
1) Găsiți domeniul funcției.
2) Se determină prezența celui de al doilea tip de puncte de pauză (vezi. Observația 1).
3) Pentru ca ecuația să găsească asymptotes înclinate
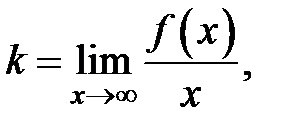
Exemplu Exemplul 2.7. Găsiți asimptota graficului:
1) Găsiți domeniul funcției
2) Ecuația asymptotes verticale deoarece
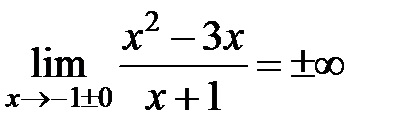
3) Ecuația asymptotes înclinate
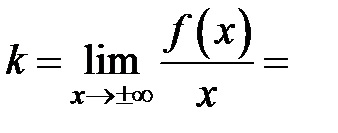
Deci - asimptotă oblică a funcțiilor graficului.
2) - o asimptotă verticală, ca
3) să clarifice problema prezenței asimptota înclinată la deoarece funcția este definită numai pentru
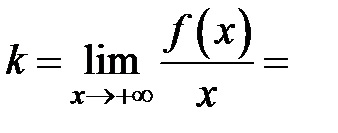
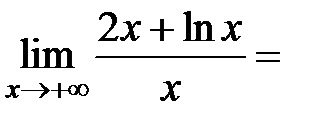
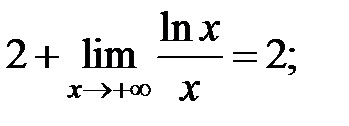
În consecință, graficul acestei funcții nu este asymptotes înclinate (vezi. Teorema 4).