Poliedru se numește o prisma, două fețe de care sunt poligoane egale situate în planuri paralele, în timp ce cealaltă parte - paralelograme având laturile comune ale acestor poligoane. Aceste paralelograme sunt numite fețele laterale ale prismei, iar celelalte două poligonului sunt numite bazele sale.
Prism este un caz particular al cilindrului. O cutie este un caz special al prismei.
Prisma are următoarea proprietate:
Orice prisme cu secțiune plan paralel cu baza sa, această prismă împarte în două prisme, astfel încât raportul dintre suprafețele laterale și raportul volum al prismelor este egal cu raportul dintre lungimile muchiilor lor laterale. Orice secțiune a planului prismei paralel cu muchia sa laterală și împarte acest lucru în două prisme prismei, astfel încât raportul dintre volumele acestor prisme este egal cu raportul dintre lungimile muchiilor lor laterale. Orice secțiune a planului prismei paralel cu muchia sa laterală și împarte acest lucru în două prisme prismei, astfel încât raportul dintre volumele acestor prisme este egală cu raportul dintre suprafața lor de bază.
tipuri de prisme
Prism. Marginile laterale ale unei prisme drepte sunt perpendiculare pe planul de bază.
prismă Oblique. Marginile laterale ale prismei sunt înclinate în raport cu planul de bază la un unghi diferit de 90 $ ^ \ $ Circ.
Corectă prisma. Baza unei prisme drepte este un poligon regulat. fețele sale laterale - dreptunghiuri egale.
poliedru semiregulate se numește un drept fețele laterale ale prismei care - pătrate.
Volumul de prisme drepte
Pentru a obține formule de calcul a volumului ia prismă prismă regulată a cărei bază este triunghi. Termina-l la un paralelipiped dreptunghiular (figura 1).
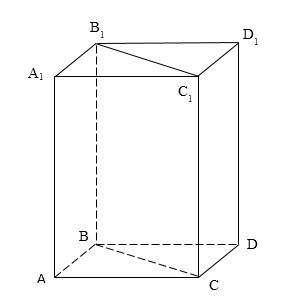
Figura 1. Un tetraedru, neterminat până la caseta
În capitolul anterior, știm că volumul unui paralelipiped este egal cu:
pentru că paralelipiped obținut compus din prisma originala si prismei, egal cu acesta în volum, volumul prismei original va fi egală cu
unde $ a $, $ b $, $ c $ lungime fete $ AB $, $ BC $, $ AC $, respectiv, iar produsul lor este egală cu suprafața inițială a bazei prismei, apoi scrisă sub forma generală a unui volum drept formulă constatare prisme:
unde $ S_ $ - baza pătrată prisma, $ H $ - înălțimea realizată la baza prismei.
Această formulă este corectă pentru oricare dintre prisme drepte cu o bază poligonală.
Volum prismă înclinată
Pentru derivarea de a găsi volum oblice prisme triunghiulare, ia în considerare prismă înclinată $ ABCDFE $. Egal printr-un plan de margine $ DC $ $ \ alpha $, perpendicular pe baza de $ ABCD $ prismei inițială și construirea unei prisme triunghiulare trunchiată (Figura 2).
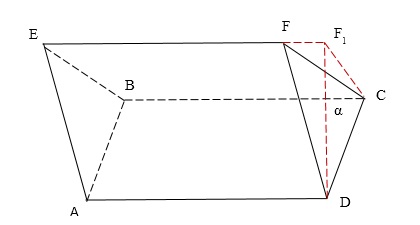
Figura 2. prismă Oblique plan $ \ alpha $
Acum, prin marginea $ AB $ plan cheltui $ \ beta $, $ a paralel plan \ alpha $ (Figura 3).
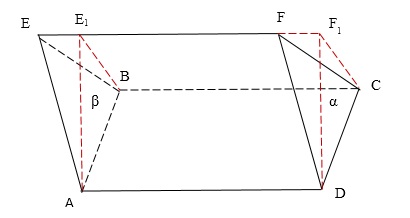
Figura 3. Oblique prismă plan $ \ alpha $ și $ \ beta $
Dacă aplicați o transformare la înclinarea feței din nou, apoi rândul său, prisma, ale cărei fețe laterale perpendicular pe bază. întoarse din nou prisme drepte.
Dacă acesta este supus unor transformări similare (suplimentează mai întâi întâi prismă trunchiate, apoi se taie oa doua prisma trunchiat), neterminat și taie prisme sunt aliniate translație paralelă pe segmentul $ AB $. Rezultă că cifrele au același volum.
Volumul În consecință, volumul unei prisme drepte este construită inițial înclinată.