Cu un număr mare de noduri de interpolare trebuie să utilizeze un grad ridicat interpolarea polinoame, ceea ce creează unele inconveniente în calcul. Puteți evita un înalt grad de interpolare segment de interpolare polinomială de rupere în mai multe bucăți, cu construirea fiecărui polinomului de interpolare independentă. Cu toate acestea, o astfel de interpolare are un dezavantaj semnificativ: punctele diferite de reticulare interpolarea polinoame este primul derivat discontinuă al acestora, astfel încât să rezolve problema de interpolare liniară folosind un porțiuni tip special de interpolare polinomiale porțiuni - spline de interpolare.
Spline - o funcție care pe fiecare interval parțial este o interpolare polinom algebric și continuu peste intervalul dat, împreună cu mai mulți dintre derivații săi.
Să se definește prin valorile sale la nodurile interpolate funcția f (x). . Notăm lungimea segmentului parțial. Noi căutăm spline în fiecare dintre segmentele parțial sub formă de:
în cazul în care - cei patru coeficienți necunoscuți. Putem dovedi că problema de a găsi spline are o soluție unică.
Necesită o coincidență a valorilor în nodurile cu valorile tabelare ale funcției:
Numărul acestor ecuații (2n) este de două ori mai mic decât numărul de coeficienți necunoscuți. Pentru a obține condiții suplimentare, avem nevoie, de asemenea, continuitatea prima și a doua derivații din spline în toate punctele, inclusiv nodurile. Pentru aceasta ar trebui să fie echivalate la derivații stânga și din dreapta. . . în nodul intern.
Calcularea expresiei pentru derivații. diferențierea succesivă (5.27):
găsi dreapta și derivații stânga la nodul:
Vom proceda în mod analog pentru a doua derivata:
Asimilarea derivații din stânga și din dreapta, obținem:
Ecuațiile (5.32) (5.33) dă încă 2 (n -1) condiții. impune cerințe privind comportamentul interpolării spline la capetele segmentului pentru a obține ecuațiile lipsă. În cazul în care cererea de la zero curbură la capetele unui interval de interpolare spline (adică, al doilea derivat egal cu zero), obținem:
Eliminarea din ecuațiile (5.28) - (5.33) n necunoscutele. vom obține un sistem de ecuații:
Sistemul (5.35) este compus din ecuații 3n. Scapati sistemul (5.35), obținem valorile necunoscut. determinarea mulțimea tuturor formulelor pentru spline interpolare necesară
Programul de punere în aplicare a metodei de interpolare spline este destul de greoaie, așa că ne limităm discuția pentru a rezolva problema de interpolare a sinusului folosind spline folosind Mathcad caracteristici pachet: interp (VS, x, y, z), lspline (x, y), pspline (x , y), cspline (x, y).
Pachetul Document MathCAD, care cuprinde o soluție de interpolare spline, constă din următoarele blocuri.
1. Setarea funcției de valori de masă interpolate
2. Calculul coeficienților spline se apropie de punctul de delimitare este o linie dreaptă, parabolică, polinomială de gradul III, respectiv.
3. Target grid discrete pentru calcularea valorilor spline
Np: = 1000 i: = 0. Np Xi: = np
4. Calculul spline valorilor la punctele de rețea
5. Vizualizarea spline (Fig. 5.6)
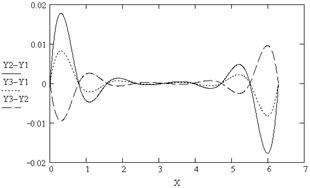
6. Construcția diferenței dintre canelurile de diferite tipuri în nodurile de rețea (Fig. 5.7)
7. Calcularea valorilor primilor derivați ai canelurilor

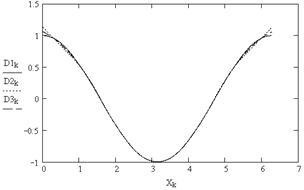
8. Trasarea derivatele primul spline (Fig. 5.8)
9. Calcularea valorilor din al doilea derivaților canelurilor
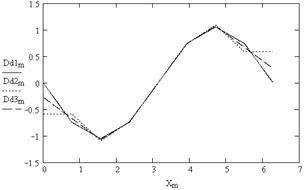
9. Trasarea derivatele doua spline (Fig. 5.9)
10. Calcularea valorilor terțe instrumentelor financiare derivate canelurile
11. Trasarea a treia derivații canelurilor (Fig. 5.10)
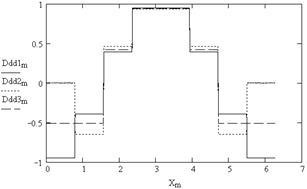
După cum se poate observa din Fig. 5.8-5.10, primul și al doilea sunt derivați de funcții spline continue, derivate de ordin superior terțe și - funcții discontinue.