În cursul aritmetică a constatat că scăderea este o acțiune opusă adăugării, prin care pentru o anumită cantitate dintr-un termen și pentru a găsi un alt termen.
Folosind această definiție, trebuie să înțelegem modul de a efectua numere relative scădere.
Să este necesar din (8) ca o deducere (3), t. E. Este necesar să se lase
În primul rând, acest număr exprimă această sumă, al doilea - acest termen, și peste pentru a găsi un alt termen (pentru a părăsit locul după semnul egal), adică este necesar pentru a rezolva întrebarea: cât de multe este necesar să se stabilească (-3) la suma sa dovedit (.. 8)? Această întrebare poate fi scrisă în această formă:
Dar, odată ce problema este dificil de rezolvat, și, prin urmare, mai întâi a rezolva o întrebare simplă auxiliar: cât de multe este necesar să se stabilească (-3), în valoare de a obține zero. t. e.
La această întrebare, răspunsul este clar: trebuie să luăm pentru numărul necunoscut pe termen având aceeași valoare absolută, deoarece acest termen, dar semnul opus - în acest caz, este necesar un termen necunoscut pentru a lua numărul trei. Ne întoarcem acum pentru a aborda problema principală: am luat pentru numărul termen necunoscut + 3, iar suma vom obține zero, dar avem nevoie pentru a obține un total de numărul 8, deci trebuie să și alți termeni au inclus același număr de opt. Prin urmare, termenul necunoscut trebuie sa fie: 1) de la 3 la zero în sumă întoarse și 2), de la 8 la această sumă „zero“ pentru a aduce până la opt necesar. Prin urmare, în locul unui termen de scriere necunoscută + 3 + 8:
(+ 8) - (- 3) = + 3 + 8 = + 11.
Acestea din urmă (= 11 +) este scrisă pe baza faptului că numărul de + 3 și + 8 trebuie să fie conectat la unul sau pliat.
Iată câteva exemple:
(- 7) - (+ 5) = - 5 - 7 = - 12.
Termenul cautat trebuie sa cuprinda 1) -5, în valoare de a obține zero și 2) de la -7 la pad zero la cantitatea necesară până la -7. Adăugarea numerelor -5 și -7, -12 obține.
(- 3) - (- 8) = 8 + - + 3 = 5.
Termenul cautat trebuie sa fie: 1) de 8, într-o cantitate pentru a obține zero și 2) de la -3 la pad zero la cantitatea necesară pentru -3. Adăugarea numerelor 8 și -3, 5 obține.
Termenul cautat ar trebui să constea 1) -9, în valoare de a obține zero și 2) 7 pentru a finaliza acest zero la cantitatea necesară pentru +7; Numerele îndoite -9 și 7, obținem -2.
Din aceste exemple, vom vedea că scăderea în algebra constă numai în capacitatea de a dezvălui paranteze ar trebui să fie al doilea număr (acest termen sau scăzut) pentru a scrie cu semnul opus, iar primul număr (această sumă sau scade), pentru a scrie cu același semn. Odată ce acest lucru este făcut, adică. E. Când paranteze sunt prezentate, problema se reduce la adăugarea, deoarece numărul scris lângă caracterele lor, de exemplu. în ultimul exemplu: - 9 + 7.
Având în vedere că suma nu este modificată prin rearanjarea termeni putem numere obținute în exemplele dezasamblate după extinderea, rearanjate la ordinea datelor a fost în acord cu numerele de ordine:
(+ 8) - (- 3) = + 8 + 3; (- 7) - (+ 5) = - 7 - 5;
- 3 - (- 8) = - 3 + 8; (+ 7) - (+ 9) = + 7 - 9.
pentru a deschide parantezele în scădere, este necesar mai întâi numărul (scade) pentru a scrie fără modificări și să atribuie un al doilea număr (scăzut) cu semnul opus.
De asemenea, observăm că atunci când se referă, pentru a scădea primul număr este scris de multe ori fără paranteze, iar dacă este pozitiv, atunci, așa cum deja cunoscut, semnul + în fața dumneavoastră nu se poate scrie.
- 3 - (- 5) = - 3 + 5 = + 2; 1 - (- 6) = 1 + 6 = 7;
3 - (3) = 3 - 3 = 0.
14. Exemple de adunare și scădere. Să presupunem că doriți să se calculeze:
Vom fi ghidați prin următoarea procedură: în cazul în care în interiorul o pereche de paranteze și paranteze sunt nici o alta nu există nici o acțiune, aceste paranteze pot fi deschise; în cazul în care în aceste paranteze este acțiunea (plus), este necesar să-l îndeplinească mai întâi. În exemplul nostru, această ordine: În primul rând, urmați de adăugarea de numere, scrise între paranteze mici, iar apoi au aceste paranteze deschise, nu matematica in interiorul parantezelor, pentru a deschide paranteze, nu matematica din interiorul paranteze răsucite, deschide aceste paranteze, și în cele din urmă stabilesc numerele rezultate:
Desigur, în cazul în care abilitatea poate efectua mai multe acțiuni simultan și, astfel, să scurteze calculul.
Un alt exemplu:

Să presupunem în continuare că doriți să evalueze expresia:
Efectuați calcule de acțiune:
1) b - c = + 1 - (4) = 1 - 4 = - 3;
2) e + f = (- 7) + (+ 2) = - + 7 = 2 - 5;
3) d + (- 5) = - 5 + (- 5) = - 5 - 5 = - 10;
4) (- 3) - (- 10) = - 3 + 10 + 7 =;
5) - 3 - (7) = - 3 - 7 = - 10.
Exemple de exerciții:
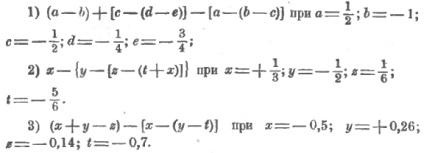
Dacă luăm numărul zero și adăugați-l de unul, vom obține o serie de creștere treptat numere întregi:
Această serie este aceeași (a se vedea. Sfârșitul paragrafului. 10) de lângă numere naturale, m. E. Cu
Dacă am luat numărul de zero, scad (1), apoi din nou scade (1), și așa mai departe. E., în conformitate cu modul în care noi o înțelegem în aritmetica în ceea ce privește numerele naturale, acum recunoaștem că aici, să ne obține toate numere întregi în scădere:
1) 0 - (+ 1) = - 1; 2) (- 1) - (k + 1) = - 1 - 1 = - 2;
3) (- 2) - (k + 1) = - 3, etc ...
Noi plecăm de la zero la stânga, scăderea numărului relativ de numere:
.... - 5 - 4 - 3 - 2 - 1, 0.
Combinând acest lucru cu seriile anterioare, obținem gama completă de numere relative:
Acest rând și la dreapta și la stânga este fără sfârșit.
Fiecare număr în această linie mai mult decât cealaltă, care stă la stânga, și mai puțin decât orice, stând în picioare la dreapta acestuia. De la 1> -3; 0> -6; -5 <0; –3 <+2 и т. д.
Între numerele întregi din această serie, aveți posibilitatea să inserați un număr infinit de numere fracționare.