Distanța dintre centrele razelor cercurilor 1 și 9 este egal cu 17. Aceste cercuri și tangente lor interioară comună ceea ce privește al treilea cerc.
a) Să se arate că linia sa de tangență cu punctul coincide cu punctul de tangență al unuia dintre primele două cercuri.
b) Găsiți raza celui de al treilea cerc.
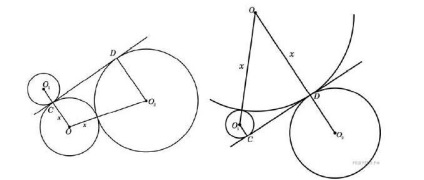
a) Fie x raza cercului necesar O centrul său. CD cercuri tangente interne de date O1 și O2 - centrele lor. Rețineți că linia CD - o tangentă externă comună a cercurilor cu centrele O și O 2 (Fig ..), sau cercuri cu centrele O și O1 (Fig ..). În acest moment se atinge coincide drepte cu punctul de tangență al primului unul din cele două cercuri, deoarece tangenta va trece printr-un punct comun (punctul de tangență) cercuri.
b) Pentru a determina raza al treilea cerc întâi dovedesc propoziția următoare. Dacă distanța între centrele cercurilor de raze R și r, a⩾r + R, o tangentă externă comună este tangent la cercurile de la punctele A și B, interior la punctele C și D, atunci
AB = sqrt (a ^ 2- (R-r) ^ 2), CD = sqrt (a ^ 2- (R + r) ^ 2).
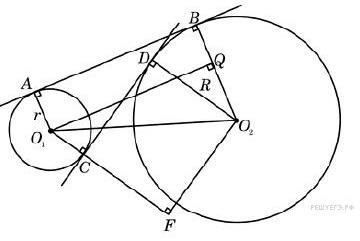
Într-adevăr, să presupunem că centrele O1 și O2 din cercuri de raze r și R, respectiv (a se vedea. Figura 2). Dintre punctele O1 și O2 O1Q picătură o perpendicular pe calea cea dreaptă O2V O2F un O1S direct. Din triunghiuri in unghi drept si O1QO2 O1FO2 descoperim că
O1Q = sqrt (O1O2 ^ 2-QO2 ^ 2) = sqrt (a ^ 2- (Rr) ^ 2), O2F = sqrt (^ 2-FO1 ^ 2 O1O2) -sqrt (a ^ 2- (R + r) ^ 2).
În consecință, CD = O2F = sqrt (a ^ 2- (R + r) ^ 2).
Prin cele de mai sus CD = sqrt (17 ^ 2 (1 + 9) ^ 2) = sqrt ((17-10) (17 + 10)) = sqrt (7 * 27) = 3sqrt (21)
În primul caz tangenta extern CD comun unui cerc cu centrul O și O2, deci CD = sqrt ((x + 9) = 2- (9-x) ^ 2) = 6sqrt (x)
6sqrt (x) = 3sqrt (21)
2sqrt (x) = sqrt (21)
4 = 21
x = 5,25
În al doilea caz tangent CD externă comună a cercurilor cu O centre și O1, deci CD = sqrt ((x + 2) = 2- (2-x) ^ 2) = 2sqrt (x)
2sqrt (x) = 3sqrt (21)
4x = 189
x = 47,25
trimite + inregistrare într-un singur clic