Tijele 3, 7, 11 - sunt numite montanți. Terminal 1, 4, 9, 12 - sunt numite acolade.
Lansete, formând un triunghi închis, numit panoul fermei.
Ferma din Fig. 56 are șase panouri.
La calcularea fermei ia pe următoarele ipoteze.
1. Toate drepte tije agricole și imponderabilitate.
2. Unități agricole - balamale ideale.
3. forțe externe sunt aplicate la nodurile fermei.
4. Ferma tije percepe numai forțele longitudinale: compresiune sau de tensiune.
Calculul fermei este de a determina reacțiile de sprijin și a forțelor interne din tije agricole.
La calcularea reacțiilor de susținere fermă este văzută ca un corp solid, care acționează asupra sistemului plat al forțelor. Calculul este de a elabora o schemă de proiectare, prepararea ecuațiile de echilibru și determinarea reacțiilor necunoscute.
Forțele din ferma tije sunt determinate:
1. Metoda unităților de tăiere.
2. Metoda secțiunilor (metoda Ritter).
La elaborarea schemelor de proiectare trebuie să se țină seama de faptul că în cazul în care tija se extinde, forța cu care acționează asupra nodului, direcționat de la nodul la terminal. Dacă tija este comprimată, forța este îndreptată spre nodul tijei (Fig. 57).
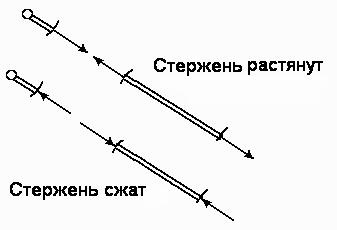
Metoda limfadenectomie
Metoda nod excizia este secvențială situri de tăiere și revizuirea echilibrul lor. Deoarece un nod acționează convergente sistem plat al forțelor la care este posibil să se înregistreze numai două ecuații de echilibru, nodurile trebuie tăiate, astfel încât o forță necunoscută a fost nu mai mult de două. presupunem că la elaborarea unei scheme de design care se întindea toate tijele, și anume toate eforturile interne în dreapta nodului la terminal. Pentru fiecare nod compus din ecuația de echilibru
În cazul în care forțele în barurile găsite în aceste formule au semnul „+“, atunci punct de vedere tehnic aceasta indică faptul că tija este întinsă, în cazul în care semnul de efort „-“, atunci tija este comprimat.
Metoda secțiunilor (metoda Ritter) este că ferma este tăiat în două părți. O parte a fermei este scăzut, și este afișat acțiunea sa în eforturile de restul tije, care sunt prinse în secțiunea transversală. Forțele din tijele sunt ghidate de-a lungul

tije la partea a scăzut jachetei, care Din nou, presupunem că toate barele sunt extinse. parte considerate ca având ferma, care sunt active (predeterminate) forță, iar forțele de reacție de susținere în tije este în echilibru. Acesta conduce la un sistem arbitrar de putere plat (nu convergent), pentru care putem scrie trei ecuații de echilibru. Prin urmare, forțele necunoscute din secțiunea nu trebuie să fie mai mult de trei.
După cum știți, există trei forme ale ecuațiilor de echilibru pentru un sistem de plat:
La elaborarea ecuațiilor de echilibru este selectat, forma care vă permite să obțineți ecuația cea mai simplă. De exemplu, dacă o secțiune transversală, două forțe necunoscute sunt paralele, este convenabil să se aplice două forma ecuațiilor. Dacă toată puterea în secțiunea disjuncte, a treia formă. În acest caz, punctele forte intersecție sunt selectate ca punct de cuplu. Astfel obținut fiecare ecuație de echilibru va conține o singură necunoscută. Comparativ cu metoda unităților de tăiere este semnificativ accelerează de calcul și crește precizia calculelor.
În cazul în care secțiunea este mai mult de trei forțe necunoscute, trebuie să efectueze secțiuni suplimentare.
Un exemplu de rezolvare a problemei
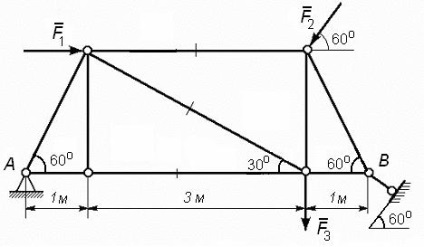
La fermă, așa cum se arată în Fig. 58, există forțe F 1 = 1 kN, F 2 = F 2 kN și 3 kN = 3.
Pentru a determina suporturi de reacție, forțe în tije prin tăierea site-uri agricole. Pentru a verifica tije marcate de eforturile depuse de secțiuni.
Toate scrisorile reprezintă unități și tije figuri. Aruncați toate suporturile și să le înlocuiască cu suportul de reacție N 1. N 2 și N B.
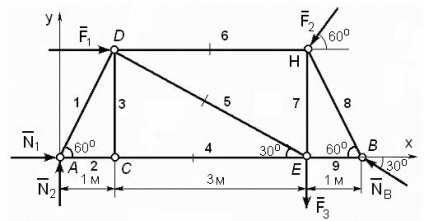
Vom arăta axele de coordonate. Schema de calcul rezultat este prezentat în Fig. 59.
Să verificați ferma pe static determinată. Ferma are 6 noduri și tije 9, adică Y = 6, C = 9. Înlocuind aceste valori în formula C = 2Y - 3, 9 obține identitatea = 2 • 6 - 3 = 9. Ferma static determinată.
Pentru a determina reacțiile de sprijin face uz de prima formă a ecuațiilor de echilibru pentru un sistem de forțe plane.
Σ F kx = N 1 + F 1 - F 2 cos60 0 - N B cos30 = 0 0;
Σ F ky = N 2 - F 2 sin60 o - F 3 - N B sin30 o = 0;
Σ M A (F k) = - F tg 60 1 1 o + F 1 2 cos60 o tg 60 o - F 2 sin60 o 4 - - F 4 Martie - N B sin30 o 5 = 0.
N = 1 - F 1 + F 2 cos60 o + N B cos30 o = -1+ 2 0,5 + 7,571 = 0,866 = -1 + 1 + 6,557 = 6,557kN.
N = 2 + F 2 sin60 o + F 3 - N B sin30 o = 2 + 3 0.866 - 0.5 = = 7.571 1.732 + 3 - 3.785 = 0,947 kN.
Astfel, N 1 = 6, 557 kN, N 2 = 0,947 kN, N B = 7.571 kN.
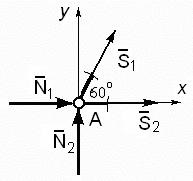
Acum definim forțele în barele de tăiere nodurile fermei. Ansamblu de tăiere rădăcină poate fi A sau nodul B, deoarece acestea nu sunt cunoscute efort doar două terminale. Să începem cu nodul A. Tăiați nodul A și ia în considerare echilibrul. La nod acte sistem de forțe convergente: a polilor de reacție N 1 și N 2 și forță din tijă 1 - S 1 și tija 2 - S 2. Eforturile urmăresc tijele din nodul spre tijele respective, adică presupunem că aceste tije sunt întinse. La punctul Un loc originea sistemului de coordonate rectangulare Axy. Schema de calcul pentru nodul A este prezentat în Fig. 60.
În acest caz, ecuațiile de echilibru sunt
Σ F kx = N 1 + S 1 + S cos60 aproximativ 2 = 0;
Σ F ky = N 2 + S 1 sin60 = 0.
Din a doua ecuație

S = 1 - păcat N 2 60 O = - 0,947 0,866 = -1,093 kN.
Din prima ecuație găsim
S 2 = - N1 - S 1 cos60 O = -6557 - (- 1,093) 0,5 = -6,01 kN.
Semnul „-“ indică în mod oficial că ambele tije sunt comprimate.
Deoarece forța în tija 2 este găsit, este posibil să se deplaseze pe la nodul C. In acest caz, forțele necunoscute în barele 3, 4 - S 3. S 4.
Tăiați și formează schema de calcul C nodului pentru el, de asemenea, așa cum sa făcut pentru nodul A (Fig. 61).
ecuațiile de echilibru sunt
Σ F kx = - S 2 „+ S 4 = 0,
Deoarece S 2 \ = S 2 = -6,01kN. atunci ecuațiile vom găsi
S 4 = S 2 „= -6.01 kN. S 3 = 0.
În consecință, tija 4 este comprimat iar tija 3 eforturile acolo. Taie un nod de circuit D. Calculat este prezentată în Fig. 62.
Necunoscutele aici sunt forțe în barele 5 și 6 - S 5. S 6.
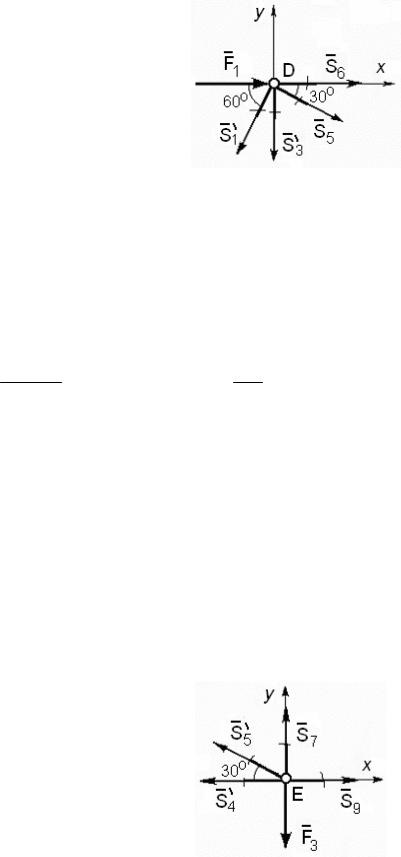
ecuațiile de echilibru sunt
Σ F kx = F 1 - S 1 „cos60 0 cos30 + S + 5 S 6 0 = 0,
Σ F ky = - S 1 'sin60 0 - S 3' - S 5 0 sin30 = 0.
Deoarece S 1 \ = S 1 = -1,093kN. S 3 \ = S 3 = 0, atunci vom găsi din ecuațiile
S 5 = sin30 1 0 (- S 1 'sin60 0 - S 3') = 0,5 1 - (-1.093) 0.866 - 0 = 1.893 kN. S 6 = - F 1 + S 1 „cos60 0 - S 0 = 5 cos30
= -1 + (- 1,093) 0.5 -1.893 0.866 = -3.186 kN.
Tija 5 se extinde, tija 6 este comprimată.
Din moment ce se găsesc forțele în barurile 4, 5 și 6, puteți continua
Taie nodul de circuit E. calculat pentru ea este prezentată în Fig. 63. Necunoscutele aici sunt forțe în tijele 7 și 9 - S 7. S 9.
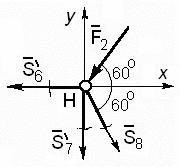
ecuațiile de echilibru sunt
Σ F kx = - S 4 '- S 5' cos30 + S 0 9 = 0,
Σ F ky = S 5 „sin30 0 + S 7 - F 3 = 0.
Deoarece S '4 = S 4 = -6.01 kN și S' = 5 S 5 = 1,893 kN. atunci ecuațiile vom găsi
9 S 4 = S '+ S 5' cos30 = 6,01 + 0 1.893 0.866 = -4.371 kN. 7 = F S 3 - S 5 „sin30 0 = 3 -1.893 0.5 = 2.054 kN.
Tija 7 este prelungită, iar tija 9 este comprimată.
Tăiați schema de calcul H. nod pentru acesta este prezentat în ris.64. Necunoscut aici este forța în tijele 8 - S 8.
ecuația de echilibru pentru site-ul sunt de forma
Σ F kx = - S 6 „- F 2 cos60 0 + S 8 0 cos60 = 0,
Σ F ky = - S 7 „- S 8 sin60 0 - F 2 0 sin60 = 0.
Deoarece S „6 = S 6 = -3.186 kN. apoi prima ecuație găsim
S 7 „= - S 8 sin60 0 - F 2 sin60 = 0 - (- 4.372) .866-.866 2 = 2,054 kN.
Eforturile în tija 7, are ca rezultat tăierea nodurilor E și H, sunt aliniate.
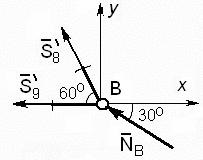
Nodul B poate fi folosit pentru a testa performanța calculelor. Tăiați Nodul B și ia în considerare echilibrul. Forțele din tijele 8 și 9 vor fi considerate necunoscute. Din ecuațiile de echilibru pentru Nodul B definesc aceste eforturi. În cazul în care acestea coincid cu eforturile aferente, constatate mai sus, calculul este corect - dacă nu, ar trebui să caute erori în calculele anterioare. Schema de calcul pentru nodul B este prezentată în Fig. 65.
Ecuația de echilibru pentru nodul B au forma
Σ F kx = - S 9 '- S 8' cos60 0 - N B cos30 0 = 0,
Σ F ky = S 8 „sin60 0 + N B sin30 0 = 0.
Rezolvarea acestui sistem de ecuații, găsim