1. Metoda de proiecție ortogonală
4. Întrebări și sarcini
O proiecție ortogonală
În cazul în care informațiile privind distanța unui punct în raport cu planul de proiecție care nu utilizează marca numerică, și prin al doilea punct de proiecție, construit pe al doilea plan de proiecție, cifra menționată la dvuhkartinnym sau complex. Principiile de bază ale acestor desene sunt prezentate Gaspard Monge - maior geometru francez al 18-lea, 19 de secole timpurii, 1789-1818 gg. unul dintre fondatorii celebrului Ecole Polytechnique din Paris și a participat la lucrările privind introducerea sistemului metric de greutăți și măsuri.
Metoda descrisă Monge proiecția ortogonală în două plane reciproc perpendiculare de proiecție a fost și rămâne o metodă primară de compilare desene tehnice.
În conformitate cu metoda propusă de Monge considerăm în spațiul doi reciproc perpendiculare pe planul de proiecție.
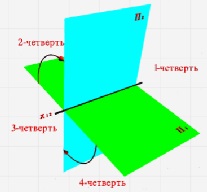
Unul dintre avioane au P1 o proiecție orizontală, iar al doilea P2 - vertical. P1 - un plan orizontal de proiecție, P2 - față. Avioanele sunt infinite și opace.
planul de proiecție a împărți spațiul în patru unghi diedru - trimestru. Luând în considerare proiecțiile ortogonale sugerează că observatorul este în primul trimestru, la o distanță infinită de planul de proiecție (fig. 89).
proiecție linie plană intersecție se numește axa de coordonate și este indicată de X21.
Din moment ce aceste planuri sunt opace, atunci doar vizibile obiecte geometrice va fi pentru observator, care sunt localizate în interiorul aceluiași primul cadran.
Pentru a obține desen plat constând în planul de proiecție P1 x12 rotație menționat combinat în jurul axei cu P2 plan. Un desen care prezintă un plan de proiecție, cu toate proiecțiile din care le descriu, combinate într-un anumit fel una față de alta, numita diagrame Monge sau desen complex.
obiecte geometrice sunt împărțite în: liniar (punct, linie, plan), neliniare (curba, suprafață) și compus (poliedre, unidimensionale și contururile bidimensionale).
Complexitatea geometrică a oricărui obiect poate fi privit ca locul geometric al punctelor de comun acord, care poate face o reprezentare a obiectului, și amplasarea lor în sistemul de coordonate poate judeca poziția sa în spațiu.
Punctul - unul dintre conceptele de bază ale geometriei. Sistematizat Geometria punctului de prezentare este de obicei presupune unul dintre conceptele de bază.
Un punct într-un sistem de două planuri ortogonale de proiecție
În construirea proiecției trebuie amintit că proiecția ortogonală a unui punct de pe planul de bază este perpendiculară a scăzut de la un anumit punct de pe acest plan. La punctul A din proiecții A1 și A2 sale ortogonale, care sunt denumite, respectiv, proiecții orizontale și frontale.
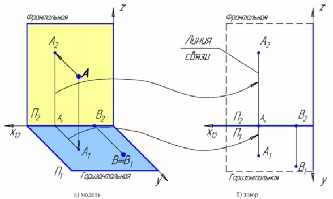
Liniile drepte care leagă proiecția ortogonală, spre deosebire de la un punct numit liniile de proiecție de comunicare.
Punctul în trei planuri ortogonale ale sistemului de proiecție,
În practică, imagini de diferite obiecte geometrice pentru a face desenul mai clar, este nevoie de a utiliza un al treilea - un plan de proiecție profilat S3, perpendicular pe P1 IP2. Proiecțiile plan P1. P2 și P3 sunt principalele planuri ale proeminențelor (Fig. 91).
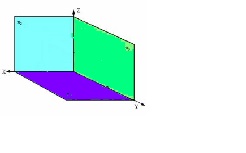
Proiecțiile punctelor de pe acest plan sunt notate cu litere latine de capital sau numerale cu indicele 3.
Plan de proiecție, se intersectează în perechi, determină trei axe Ox. Oy și Oz, care poate fi considerat ca un sistem de coordonate carteziene în spațiu cu punctul 0 de pornire.
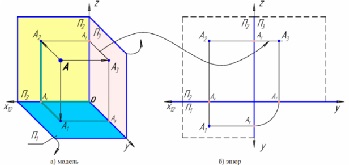
Pentru punctele de diagrama din planul trei planuri P1 și P3 de proiecție este rotit pentru a se alinia cu P2 plan. Atunci când desemnarea axelor pe diagrama jumătății axa negativă nu este indicată de obicei. Dacă numai obiecții în mod substanțial imaginea în sine, mai degrabă decât poziția sa în raport cu planul de proiecție, pe axa diagramei nu este prezentată (fig. 92).
Poziția tridimensională a setului punctului folosind koordinath cartezian, y și z (abscisă, ordonată și applicate).
Stat proprietatea principală a proiecțiilor ortogonale ale punctului de exemplu:
1. Două puncte definesc proiecția poziției sale în spațiu.
2. Două proiecții ale punctelor se află pe aceeași legătură.
3. Pentru două proiecții punctul pe care se poate construi un al treilea.
linie directă - unul dintre conceptele de bază ale geometriei. Prezentarea sistematică linie dreaptă geometria este, de obicei, presupune unul dintre conceptele de bază, ceea ce a determinat doar indirect geometria axiome. În cazul în care geometria este baza pentru construirea conceptului de distanța dintre două puncte în spațiu, linia dreaptă poate fi definită ca o linie de-a lungul căreia distanța dintre două puncte este cel mai scurt.
Linia dreaptă - first-order linie algebrică: linie dreaptă într-un sistem de coordonate carteziene în planul dat de ecuația 1 - lea grad (ecuație liniară).
Ecuația generală a unei linii drepte (complet): Ax + By + C = 0,
în care A, B și C - orice constantă, iar A și B nu sunt simultan egale cu zero. Dacă unul dintre coeficienții este zero, ecuația se numește incompletă.
Metode de setare grafică linie dreaptă
2. Cele două planuri (a, b).
3. Două proiecții.
4. Doza inițială și unghiurile la planele ale proeminențelor.
Situația în ceea ce privește planurile de proiecție linie dreaptă
Direct în raport cu planul de proiecție, se poate ține atât dispoziție generală și private.
1. Direct nu este paralelă cu nici un plan de proiecție se numește directă un generic.
2. planuri paralele directe ale proiecțiilor ocupă poziția specială în spațiu și sunt numite pryamymiurovnya. În funcție de ce plan de proiecție paralel cu linia de date, se disting:
2.1. Proiecțiile directe paralele plan frontal numite frontal sau frontal - n.
2.2. Drepte proeminențe orizontale paralele sunt numite orizontalelor orizontale sau - m.
2.3. Drept plan paralel profil al proiecțiilor numit profil - p.
3. Direct perpendicular pe planul de proiecție, ocupă poziția specială în spațiu și se numesc proiectate. Direct audio perpendicular pe planul de proiecție paralel cu celelalte două. În funcție de faptul dacă un plan de proiecție perpendicular anchetate drepte, se disting:
3.1. Orizontal proeminente drepte - m.
3.2. Proiectând drept frontal - n.
3.3. Profilate proeminente dreaptă - p (Figura 93.).