Obiectiv: Pentru a studia legile armonice mișcare de vibrație
zheniya exemplul unui pendul matematic.
Instrumente și accesorii: pendul matematic, cronometru, riglă.
mișcare oscilatorie (oscilație) este un proces în care sistemul este deviat în mod repetat, de la starea sa de echilibru, de fiecare dată când se întoarce la ea.
Dacă această întoarcere se face la intervale regulate, atunci se numește oscilație periodică.
Fluctuațiile sunt numite liber sau propria lor, în cazul în care apar într-un sistem lăsat să se după ce a fost scos din poziția de echilibru.
Cel mai simplu caz este oscilație periodică mișcare armonică oscilatorie.
Numită oscilație armonică, la care amplitudinea de oscilație variază în sinusul (sau cosinus):
um x = sin () (1)
In mecanica: deplasarea x a punctului oscilant din poziția sa de echilibru variază în sinusul (sau cosinus)).
Valoarea maximă a deplasării din poziția de echilibru hmm nazyvaetsyaamplitudoy oscilație armonică. Argumentul (a), care stă sub semnul sinusul (sau cosinus). Se numește oscilație de fază. a - faza inițială (la t = 0). Valoarea se numește frecvență ciclică de oscilație armonică:
Cantitatea T este perioada de oscilație - pe parcursul unui complet kolebaniya-, valoarea = 1 / T (Hz) - frecvența de oscilație - numărul de oscilații pe unitatea de timp.
Viteza de oscilație armonică Instantanee
V = = hm cos (t + o) (3)
Accelerarea. a = - 2 um sin (t + o) = - x 2 (4)
Ecuația 2 + x = 0 (5)
Se numește o ecuație diferențială de oscilații armonice. Soluția acestei ecuații în forma (1).
Armonici oscilațiile apar sub forța
F = ma = - m 2 x = - kx. unde k = m 2. (6)
proporțională cu deplasarea și direcționată spre o poziție de echilibru. Acesta poate fi, de exemplu, forța elastică (dinamometru). Forțele restabilesc pot avea, de asemenea, de altă natură, nu elastic. În aceste cazuri (pendul matematic) se numesc forțe cvasi-elastice (din cvasi latină - așa cum au fost, se presupune).
Deoarece k = m = 2. perioada de oscilație armonică poate fi calculată prin formula
Luați în considerare sistemul oscilant mecanic este un pendul matematic.
pendulul matematic este numit un punct material, sub suspendat pe un fir imponderabil și inextensibil - Figura 1.
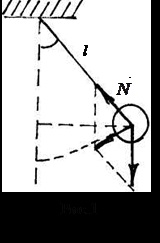
și anume la deformare mici unghiuri de forțe care cauzează vibrațiile vor fi proporționale cu deplasarea direcționată către poziția de echilibru și, prin urmare, oscilațiile pendulului va fi armonic.
Având în vedere că o = mg / l. perioada de oscilație a pendulului matematic poate fi calculată folosind următoarea formulă:
De la (8) rezultă că perioada de oscilație a pendulului matematic depinde de lungimea I a pendulului și accelerația gravitațională g. dar aceasta nu depinde de masa m pendulului și amplitudinea oscilațiilor xm
DESCRIERE INSTALARE ȘI METODĂ DE MĂSURARE
Stabilindu perioada de oscilație a pendulului matematic lungime cunoscută, se poate calcula amplitudinea accelerației gravitației în Pământului (accelerația gravitațională depinde de latitudinea geografică), prin formula
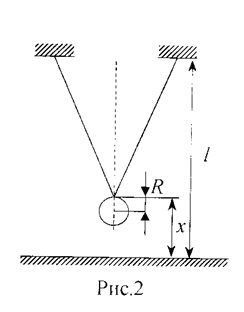
Pendulul folosit în această lucrare este o rază masivă balon mic (în comparație cu lungimea pendulului), suspendat pe un fir dublu la fluctuații posibile a apărut mai strict într-un singur plan. Distanța de la punctul de suspensie al pendulului podelei L = W, 20 m, raza bile R = 3,95 cm.
Ordinea executării
1. Pentru a determina lungimea pendulului. Pentru aceasta se măsoară distanța de la podea la partea de sus a mingii (a se vedea figura 2). Se calculează lungimea pendulului cu formula
, Stoca rezultatul în tabelul