Luați în considerare un pendul simplu - o minge suspendat pe un fir lung puternic. Un astfel de pendul se numește fizică. În cazul în care dimensiunea mingea este mult mai mică decât lungimea firului, atunci aceste dimensiuni pot fi neglijate și considerate ca mingea punct de material. Stretch fire pot fi, de asemenea, ignorate, deoarece este foarte mic. În cazul în care greutatea de fire este de multe ori mai mică decât masa bilei, greutatea firului poate fi, de asemenea, ignorate. În acest caz, avem un model al pendulului, care este un pendul matematic.
Se numește matematică material de pendul punct de masă m m. suspendate pe o imponderabilă inextensibil lungime fire L L în câmpul gravitațional (sau alte forțe).
Galileo Galiley experimental a constatat că matematic perioada pendul oscilație într-un câmp de gravitație nu depinde de masa sa și amplitudinea de oscilație (unghiul deflecției inițiale). El a constatat că perioada de oscilație este direct proporțională cu L - - √ L.
Perioada de oscilație mică pendul matematic în gravitația Pământului este definită de Huygens:
T = 2 π L g - - √. T = 2 π L g.
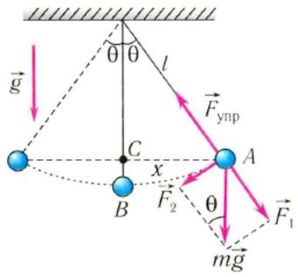
În pendul matematic deflexie unghiurile α <20 0 α <20 0 погрешность расчета периода по формуле Гюйгенса не превышает 1 % 1 %.
În general, atunci când pendulul este în domenii omogene de mai multe forțe, ar trebui să intre în „eficace accelerare» g * g * pentru a determina perioada de oscilație. caracterizarea efectele rezultante ale acestor domenii, precum și perioada de oscilație a pendulului va fi determinată prin formula
T = 2 π L g * - - - √. T = 2 π L g *.