Să presupunem că un plan infinit (Fig.3.5) este uniform încărcat cu o densitate de încărcare suprafață ( = dQ / dS este sarcina pe unitatea de suprafață).
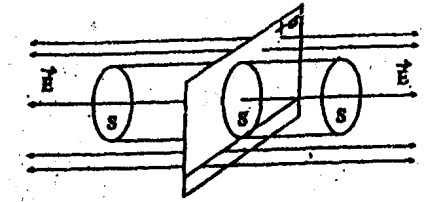
Izolați pe o suprafață plană S și înconjoară suprafața cilindrică închisă cu o bază, plan paralel. Deoarece vectorul liniei E perpendicular pe planul și paralel cu generatoarele cilindrului, debitul total printr-o suprafață cilindrică închisă este egală cu suma fluxurilor numai prin cele două baze ale sale:
Conform teoremei lui Gauss-Ostrogradskii
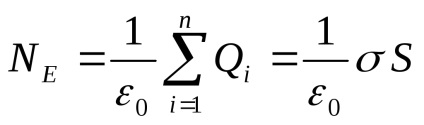
Prin echivalarea din dreapta pentru N, obținem
Din (3.11), rezultă că intensitatea câmpului a planului infinit încărcat la punctele nu depinde de distanța lor. Prin urmare, câmpul este planul omogen.
Domeniul de două planuri paralele infinite încărcate opus (figura 3.6)
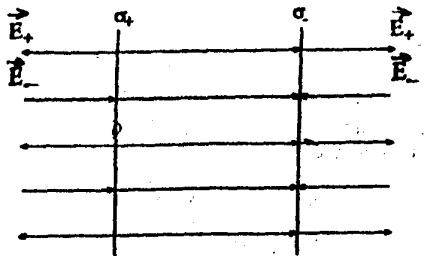
Să presupunem că planurile de suprafață cu densitate de încărcare + i -ravny cea mai mare. După cum se vede în Figura 3.6, liniile de câmp pe partea stângă și dreaptă a avionului sunt îndreptate unul spre celălalt. Prin urmare, intensitatea totală a câmpului este E = 0 avioane. În zona dintre planurile, având în vedere (3.11).
Astfel, câmpul este omogen între avioane. Și pot fi considerate ca fiind câmp omogen în interiorul plane paralele finite (plane condensator).
Lucrul forțele câmpul electrostatic atunci când se deplasează de încărcare. potențial
oh
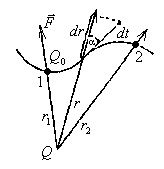
Din moment ce o taxa de mișcare puterea Q0 a interacțiunii sale cu zaryadomQ. Creează un câmp de legea lui Coulomb depinde de rasstoyaniyar:
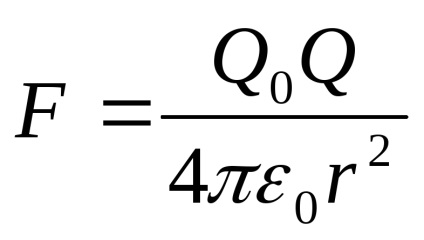
trebuie să definiți mai întâi elementar de lucru uchastkedℓ infinitezimal Dáňa:
Aici α - unghiul dintre vectorii Fidℓ. Având în vedere chtodℓcosα = dr, vom găsi performanța generală a integralei:
Rezultă că funcționarea câmpului electric nu depinde de forma traseului, așa cum este determinat de taxa inițială și pozițiile finale Q0. Acest lucru înseamnă câmp chtoelektrostaticheskoe este potențial, iar puterea - conservatoare.
(3.13) arată că activitatea desfășurată în mișcare de încărcare într-un câmp electrostatic de-a lungul oricărui contur închis este egal cu zero, adică:
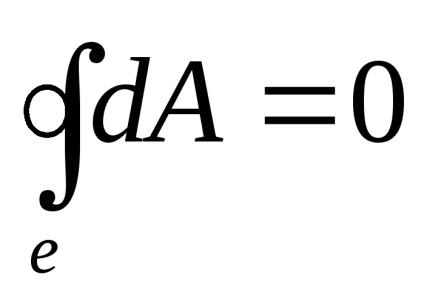
Ultima egalitate poate fi scris, având în vedere că
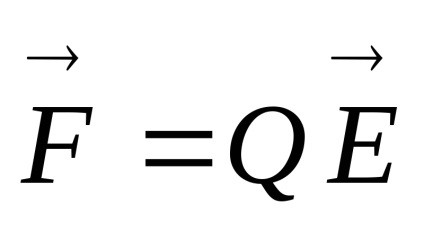
Apoi, câmpul electrostatic, avem:
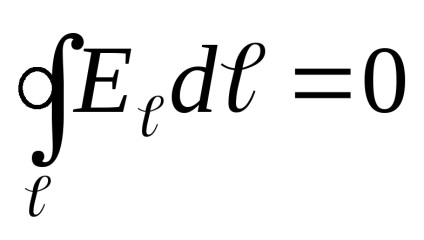
în care proiecția Eℓ = E sosα- a vectorului E în peremescheniedℓ.
Aceasta se numește integral circulația electrostatica vectorului câmp circulație napryazhennosti.Dlya de-a lungul oricărei buclă închisă zero.
Din „mecanica“, știm că activitatea forțelor conservatoare este egală cu pierderea de energie potențială:
Comparând acest lucru cu ecuația (3.13), obținem formula de încărcare Q0 energie potențială. situat în zaryadaQ:
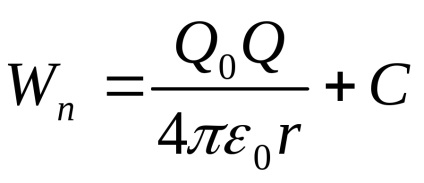
Pe măsură ce distanța de la Q de încărcare și potențiale scade de energie poate presupune că în beskonechnostiWp = 0, constanta de integrare
Raportul Wt / Q0 este independentă de încărcătura și poate sluzhitenergeticheskoy câmp caracteristic. câmp nazyvaemoypotentsialom la un anumit punct creat zaryadomQ:
Formulele (3.14) și (3.15) că potențialul unui câmp de încărcare punct (balon) Q:
Munca efectuată de către forțe electrice care se deplasează în taxa de Q0 de la punctul 1 la punctul 2, poate fi calculată prin diferența de potențiale:
Dacă punctul 2 este situat la infinit, φ2 = 0 și, prin urmare,
în cazul în care Q0 este magnitudinea taxei transportate la câmp.
Astfel, potențialul punctului a câmpului determinat de activitatea desfășurată de către forțele de câmp, atunci când se deplasează o unitate de încărcare de la acel punct la infinit. Unitatea de potențial prinyatVolt:
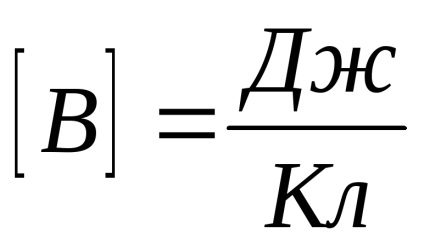
capacitatea semnului este determinată de semnul taxei, creând un câmp. În cazul în care câmpul este format dintr-un sistem de taxe, potențialul său este egală cu suma algebrică a potențialelor domenii ale tuturor taxelor (principiul superpoziției)
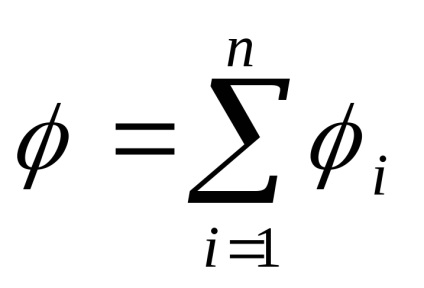
Punctul în spațiu la potențiale egale formează o suprafață numită echipotențiale. O astfel de suprafață, de exemplu, este suprafața sferei conductoare încărcată uniform.
Funcționarea la alternarea sarcină Q împreună poverhnostiA echipotențială = Q Δφ = 0.