Metoda geometriei descriptive a mișcării plane utilizate în mod normal pentru determinarea valorilor reale ale cifrelor plane, și unghiurile de segmente.
Proprietăți de circulație paralele:
- Când mutați orice figură paralelă cu planul de proiecție, cifrele de proiecție de pe acest plan rămâne neschimbat.
- Deoarece punctul paralel cu planul de proiecție orizontală, proiecția sa frontală se deplasează într-o linie dreaptă paralelă cu axa X. În figura de mai jos punctul C 'și D „“, ca urmare a acestei proprietăți și a luat poziția C''1 D“„1.
- Deoarece punctul paralel cu planul frontal al proiecției, proiecția sa orizontală se mișcă într-o linie dreaptă paralelă cu axa X.
Luați în considerare segmentul CD de transfer arbitrar dispus într-o poziție paralelă cu proiecțiile plane P2 orizontale.
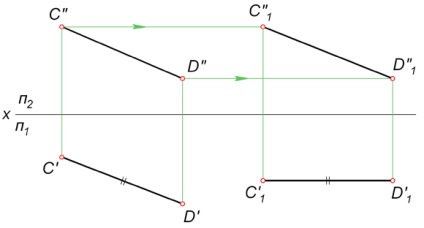
- Folosind prima proprietate a mișcării paralele, în orice loc în desen sunt construirea segmentului c'1 D'1 = C'D“.
- De-a lungul liniilor de comunicare definim C''1 de proiecție lipsește și D“„1. Săgețile indică deplasarea punctele C 'și D' paralelă cu axa X în conformitate cu o a doua caracteristică a metodei.
Următoarea figură ilustrează MN segmentul de transfer în proiectarea poziție în raport cu planul frontal proiecțiile P2. In general, pentru a rezolva această problemă este necesar să se utilizeze metoda dublă mișcare plan-paralel.
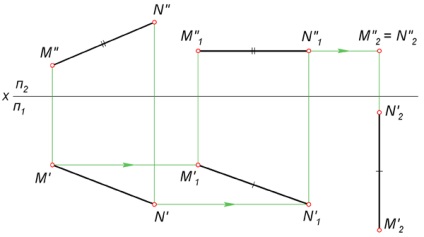
- După primul segment de conversie MN ia poziție paralelă cu planul P1. Mai întâi construite M''1 N''1 = M''N „“ într-o poziție arbitrară a desenului, și apoi prin comunicare linii lipsesc M'1 de proiecție și N'1.
- A doua transformare este o deplasare paralelă a proiecției orizontale a segmentului în poziția M'1 N'1 M'2 N '-2-. perpendicular pe axa X. După acest punct M''2 = N''2 determinată prin linii de comunicație.
Determinarea dimensiunii reale a unui triunghi
Luați în considerare ordinul unui deplasare plan paralel al triunghiului ABC pentru a determina dimensiunea reală.
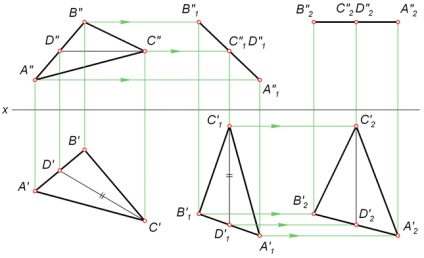
- Prin punctul C al triunghiului ABC efectuează CD-ul orizontal. Am găsit-o proiecție lipsește.
- ABC traduce într-o poziție perpendiculară pe planul frontal de proiecție. Pentru acest construct c'1 D'1 = C'D „perpendiculară pe axa X. Conform unei prime caracteristici a mișcării plan paralel fiind finalizat triunghi A'1 B'1 c'1 = A'B'C“. Liniile de comunicații definesc punctul A''1. B''1. C''1.
- Mutați proiecția A''1 B''1 C''1 ABC poziția triunghi A''2 B''2 C''2. paralelă cu axa X, după ecuația A''2 B''2 C''2 = A''1 B''1 C''1. Liniile de comunicații definesc punctul A'2. B'2. C'2. Acum triunghiul ABC este paralelă cu planul orizontal de proiecție, și este proiectat pe un full-size A'2 B'2 c'2.
Determinarea distanței dintre liniile paralele
Distanța dintre două linii paralele este lungimea perpendicularei a scăzut de la orice punct al primei linii de pe a doua linie. Luați în considerare modul în care se determină distanța de mai sus, în practică, prin metoda mișcării plane.
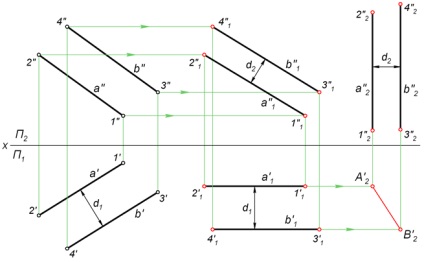
Prin două transformări succesive o directă și b sunt traduse într-o poziție perpendiculară pe un plan orizontal. Astfel, ele sunt proiectate pe ea în termeni A'2 și B'2. distanța dintre care este cel dorit. Se arată în figura valorile d1 și d2 sunt construcții auxiliare pentru a efectua în funcție de proprietățile mișcării plane.