Să ne amintim că sofismul numit raționament în mod intenționat fals că are vizibilitatea corespunzătoare.
sofisme logice - sofistică, care sunt erori în raționamentul greșit.
"Half-gol, de asemenea, și că semi-plin"
Jumătate gol este la fel ca și pe jumătate plin. În cazul în două părți egale, înseamnă, și sunt numere întregi. Prin urmare, gol este la fel ca și pe deplin
Eroare: nu este pe jumătate gol sau pe jumătate goală, apoi, și ceea ce este fie pe jumătate plin.
Luați în considerare acest sofism numit „hoț“. Acesta este formulat etsya în raționamentul că chemările-ci să ne convingă că hoțul nu contează bla Goa. Pe faptul că și sofistică de a folosi logica lui Sofistul-cal pentru a dovedi că este nedovedit.
„Hoțul dobândește un Horo-gât.
Dobândi, la fel de bine, și de a face bine - este bine.
Deci, hoțul face bine. "
Sofismă defect este vizibil din prima privire doua: să dobândească bune și de a face bine - nu numai că nu concepte echivalente, dar nici măcar sinonime.
Iată un alt sofism „om de știință KI“, care se obține din premise adevărate concluzie falsă:
„Horo-Sho Toți elevii atenți să învețe lecții.
Unii studenți atent.
Toți elevii învață lecții bune. "
sofistică matematică - o declarație uimitoare,
dovada care stau invizibile,
și erori, uneori, destul de subtile.
Mai mult sofisme logice, de asemenea, cunoscut și matematică-cal. sofistică matematică a contribuit și contribuie la rigoarea raționamentului matematic, și a ajutat la promovarea o mai bună înțelegere a conceptelor și metodelor de matematică. În opinia noastră, rolul lor în dezvoltarea matematicii este similar cu rolul pe care continuă să joace în ziua de azi erori involuntare în dovezi matematice permise chiar matematicieni restante.
Luați în considerare materialul diferit pe cercetare, am aflat că sofistică sa bazat pe conceptele de logica, legile sale, care se bazează pe presupuneri false. Dar absurditate Să se bazează pe silogism fals în mod deliberat, dar dacă îl uiți superficial, pare să fie adevărat.
În timpul lucrărilor, am aflat că Dzhordzh Bul, de asemenea, sa bazat pe noțiunea de logică în algebra. El a operat conceptele de adevărat și fals.
Dar tehnologia modernă de calculator utilizează doar false pe termen lung și adevărat. Cibernetică ca știință, și o face.
Se pare că învățăturile sofiști le folosim în viața modernă, în special în tehnologia digitală, calculatoare.
Există trei tipuri de sofisme matematice:
De obicei, sofisme matematice ascunse run-app acțiune reschennye sau fără a lua în considerare condițiile de aplicabilitate, sunt mari-lift, formule sau teoreme. Un foarte interesant în a găsi o greșeală în raționament, institute de cercetare, ceea ce duce la absurd concluzie-mu, și nu este întotdeauna lay-a și ușor de făcut.
a) sofism aritmetică
sofisme aritmetice - sunt expresii numerice care inexactități sau erori nu sunt vizibile la prima vedere.
Exemple de sofisme aritmetice sunt următoarele:
1) „De două ori două-cinci“.
Lăsați raportul de aspect original, - egalitatea evidentă:
Scos din paranteze factorul comun al fiecărui credit de egalitate (*), și obținem:
Apoi extinde numărul 4 pe activitatea de 2 × 2.
În cele din urmă, știind că 1: 1 = 1, avem de la (**) set: 2 x 2 = 5.
Eroare: eroarea constă în faptul că era imposibil să facă un factor de multiplicare luat in ecuatie (**)
2) La momentul când mama și tata erau copii, adică, în perioada sovietică,
a existat monedă, cum ar fi rubla, care este egal cu 100 de copeici. Deci, unul dintre sofismele ne spune altfel.
„O rubla nu este egal cu o sută de penny“.
Este cunoscut faptul că oricare două dintre inegalitatea poate fi multiplicată termen de termen, fără a încălca ecuația, adică Dacă a = b, c = d, atunci ac = bd.
Vom aplica această dispoziție la cele două egalitatea evidentă
Înmulțind aceste ecuații termen de termen, obținem 10 p. = 100000 polițist.
În cele din urmă, împărțind ultima ecuație 10 obținem că 1 p. = 10 000 copeici.
astfel, o RUB nu este egal cu o sută de penny.
Eroare: eroare făcută în acest sofism, este în încălcarea regulilor de acțiune cu variabile numite: toate activitățile care au loc pe cantități, este necesar să se efectueze bine pe dimensiunile lor.
3) Noi pretindem ce 5 = 6.
Este ușor de verificat ecuația fair-Ness: 35 + 10-45 = 42+ 12-54.
După ce a suferit un factor comun din paranteze, poate fi scris ca:
5 • (7 2- + 9) = 6 • (2 + 7 - 9) de.
După cum putem vedea, produsele sunt egale, iar al doilea factor este de asemenea egal, de aceea, primii factori să fie egali, adică. E. 5 = 6.
Eroare: eroare în judecătoriilor aceste rase este că am tras o concluzie cu privire la egalitatea dintre primii factori au produs un egal-TION cu condiția egalității dintre factorii secundari, aceasta nu este întotdeauna adevărat. Acest lucru este valabil numai în cazul în care regulat secară OMC factori diferiți de zero, și putem împărți ambele părți de acest număr. În cazul zero, este întotdeauna a = b · 0 · 0 = 0 pentru orice a și b, deci nu este obligatorie pentru a = b.
4) „Unitatea este egal cu doi“
scădere simplă este ușor de a verifica validitatea egalității
Adăugarea de ambele părți ale acestui număr ecuație. Obținem o nouă egalitate
în care, așa cum este ușor de văzut, din dreapta și din stânga sunt părți pătrate pline, r. f.
Extragerea din dreapta și stânga părțile laterale ale ecuației anterioare rădăcina pătrată, obținem:
ceea ce implică faptul că
b) sofistică algebrică
Algebrice sofistică - erori în mod deliberat ascunse în ecuațiile și expresiile numerice.
1) Afirmam ce 4 = 5.
Ia două numere a = 4 și b = 5, lor de jumătate de sumă este notat cu c = (a + b) / 2.
Apoi a = b și 2S- 2c-a = b.
Înmulțind această egalitate de către statele membre, obținem:
și 2 - 2AS = b 2 - b 2 c.
Adăugarea la ambele părți ale unei 2 obținem:
și 2 - Al 2 + c 2 = b 2 - b 2 + c 2
sau (a - c) 2 = (b - c) 2.
Prin urmare, a-c = b-c unde a = 6, adică 4 = 5.
Eroare: În cazul în care numerele sunt egale cu pătratele, numerele în sine nu sunt obligatorii, dar egale, ele pot fi împotriva-vopolozhnymi. Egalitatea-c = b-c, în acest caz, nu este adevărat, ar trebui să fie o c = b-a sau a - c = c - b.
Aspect general: „Toate numerele sunt egale între ele“
Ia două număr arbitrar inegal între ele a și b și scrie identitate evidente pentru a le:
și 2 -2ab + b 2 = b 2 a 2 -2ab +
Stânga și dreapta sunt pătrate perfecte, t. E. Putem scrie
Bazându-se pe ambele părți ale acestei ecuații cu rădăcina pătrată, obținem:
unde 2a = 2b sau în final, a = b.
2) Pretindem că numărul 0 (zero) pe orice număr de.
Dacă numărul este negativ, atunci afirmația este evidentă.
Să o - la fel de mult ca și numărul de durere-Choe pozitiv. Este clar că un - 1 <а.
Noi multiplica ambele părți ale acestei inegalități pe un termen de termen - mai degrabă, obținem:
Adăugarea de ambele părți ale inegalității podea chennogo și 2. să aibă: - un 2 + a + 2 <- а 2 + а 2. то есть а <0.
Prin urmare, orice, chiar și în mod arbitrar pozitiv-ing numărul și mai mică decât 0.
Eroare: Atunci când înmulțirea ambele părți ale inegalității la locul de muncă, care este un număr negativ, semnul inegalității trebuie să fie schimbat la opusul.
3) Să demonstreze că orice număr de egale, dar 0.
Luați în considerare suma: A - A + A - A + A - A + A -.
Această sumă poate fi exprimată în două moduri:
Părțile laterale stânga ale acestor expresii sunt egale, atunci egal și dreapta, și, prin urmare, o - 0.
Eroare: În prima expresie este considerată o cantitate-TION chiar și-SRI inclus de termeni, iar al doilea - nu, chiar, astfel încât rezultatele să difere, și sunt pornite.
c) sofistică geometrică
sofistică geometrică bazată pe eroarea asociată cu figuri geometrice și acțiunile pe ele.
1) „Coarda care nu trece prin centrul cercului este egal cu diametrul“.
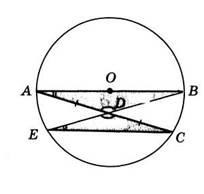
diametrul cercului realizat AB Presupunem că. Prin punctul B efectueze orice acord BE nu trece prin centrul, și apoi prin mijlocul corzilor D și punctul A va organiza o nouă coardă de curent alternativ. În cele din urmă, punctele E și C sunt conectate printr-un segment de linie.
lua în considerare # 8710; AVD și # 8710; EDS. In aceste triunghiuri: BD = DE (de construcție), <А=
= <Е (как вписанные, опирающиеся на одну и ту же дугу). Кроме того, <ВDА=
= <ЕDC (как вертикальные). Если же сторона и два угла одного треугольника соответственно равны стороне и двум углам другого треугольника, то такие треугольники равны. Значит, ∆ ВDА= ∆ЕDC. а в равных треугольниках против равных углов лежат равные стороны. Поэтому, АВ=ЕС.
Eroare. eroare este o aplicație incorectă a teoremei privind egalitatea de triunghiuri. Prin teorema pe triunghiul semnul de egalitate: în cazul în care două laterale adiacente și unghiul ei de un triunghi sunt egale cu latura și adiacent la cele două colțuri ale altor triunghi ei, atunci triunghiuri sunt egale. Și în cazul nostru, <А не прилежит к стороне ВD .
2) „Potriviți de două ori, atâta timp cât un pol de telefon.“
Lăsați un meci și lungimea b - lungimea coloanei. Diferența dintre a și b oboznachimcherez c.
Avem b - a = c, b = a + c.
Înmulțiți două părți de egalitate: b 2 - ab = Ca + c 2.
Scădeți din ambele părți bc. Obținem: b 2 - ab - bc = circa + c 2 - bc. sau
b (b - a - c) = - c (b - a - c), în cazul în care
b = - c. dar c = b - a. Prin urmare, b = a - b sau a = 2b.
Eroare: eroarea constă în faptul că vravenstve expresii b (b-a-c) = - c (b-a-c)
se împarte 0.
Acestea sunt doar câteva din set-TION cunoscut inca din cele mai vechi timpuri și au ajuns la noi sofistică logică și-ma tematice. Sofistică a ajutat să ridice rigoarea raționamentului matematic și pentru a promova o mai bună înțelegere a conceptelor și metodelor de matematică. Pentru a studia matematica sofistică utilă prin faptul că analiza lor se dezvoltă gândirea logică.
Detecta o eroare în sofismul - ceea ce înseamnă să-l realizeze, dar realizarea erorii avertizează împotriva repetarea în alte raționament matematic.
Clasificarea, am considerat sofistică, pentru erori și subiecte admise la acestea, studiul, care, în opinia noastră, acestea pot fi utilizate este reprezentat de noi în cerere.
Deci, sofismă - Această imagine-tenie mintea umană, cu Pomo-schyu pe care le poate dovedi nimic. De altfel, puteți nega, de asemenea, totul. Nu degeaba au fost-tac român om de știință I. P. Pavlov, a declarat că „a înțeles în mod corespunzător greșeală. - aceasta este calea spre descoperirea“
La început poate părea că există puține sofistică, sau că acestea nu sunt utilizate în viață, care este inutil. Dar acest lucru nu este cazul. Există o mulțime de diferite tipuri de sofisme. Și sofismele matematic - doar o mică parte din ele. În timpul vieții sale, o persoană aude zeci de sofisme, să nu poată să le distinge de declarațiile veridice, și nici măcar să știe ce înseamnă cuvântul, în general, sofistică.
Înțelege sofistică, adică să o rezolve, se pare, nu dintr-o dată. La început, pentru a aborda unele sofistică, au avut de multe ori pentru a re-citit-le cu atenție, verifică și meditați, cum ar fi sufismul „coardă, nu trece prin centrul cercului este egal cu diametrul“ a trebuit să caute mai departe pentru o eroare. Acum, la sfârșitul lucrării pe studiul de bug-uri, am început să fie mai rapid. Noi credem că o gândire logică bine dezvoltat poate ajuta nu numai in rezolvarea problemelor, ci și în viața de zi cu zi. În general, decizia sofism - interesantă și educativă. Ei pot face cu atât intenționat și în timpul lor liber pentru distracție, cum ar fi o soluție skanvordov sau Sudoku.
Aici ei sunt și aici, cum sofistică ea - sofistică. Și are propria logică, poate că nu e logic cu o majusculă, dar cel puțin logica sofistice. Și este demn să se obișnuiască cu această logică, deși este implicat în erorile logice. Dar logica de a studia legile nu sunt doar corecte, dar gândirea greșită. Pentru că este imposibil să știu este noroi, nu știe minciună, deoarece este imposibil să înțelegem binele fără să știe răul. Într-o lume ca aceasta: lumina adiacente la umbră, viață - moarte, și este de-Tina - o minciună.
Am ajuns la concluzia că sofistica matematică dezvoltă observare și chibzuința, a învățat să monitorizeze cu atenție acuratețea formulării, înregistrările corecte și desene ale legalității operațiunilor. Ei bine, și, în cele din urmă, sofismele analiză pur și simplu fascinant - aceasta gimnastica gratioase pentru mintea oricărui om.
Din moment ce nu sunt bune la crearea propriilor lor sofisme, pentru munca de cercetare, am utilizat sofismele [3]