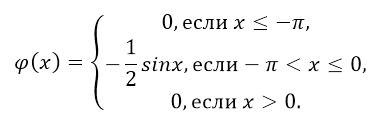Recall formula pentru a găsi probabilitatea ca intervalul variabila aleatoare ajunge $ (\ alpha, \ beta) $:
Să ne găsim probabilitatea ca o variabilă aleatoare va cădea în intervalul de $ (- \ infty, + \ infty $):
Este evident că o variabilă aleatoare intră întotdeauna în intervalul de $ (- \ infty, + \ infty $), prin urmare, probabilitatea unui astfel de contact este egal cu unu. obținem:
Geometric, a doua proprietate este aceea că aria trapezului curbiliniu delimitată de graficul distribuției densității de $ \ varphi (x) $ și axa x este numeric egal cu unu.
De asemenea, este posibil să se formuleze proprietatea opus:
Proprietatea 3: Orice non-negativ funcția $ f (x) \ ge 0 $ satisfac ecuația $ \ int \ limite ^ _ = 1 $ este o funcție a distribuției densității unei variabile aleatoare continue.
Sensul probabilistic al distribuției densității
Să ne dea variabila $ x $ $ creștere \ triunghi x $.
Sensul probabilistic al distribuției densității: Probabilitatea ca un proces continuu variabilă aleatoare X $ $ ia valori de la $ interval (x, x + \ triunghi x) $, este aproximativ egală cu produsul densității de probabilitate în punctul $ x $ pentru incrementarea $ \ triunghi x $:
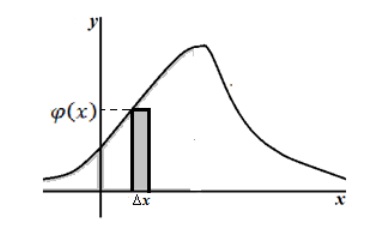
Figura 4. sensul probabilist de distribuție aleatorie continuă geometrică variabilă Vector densitate.
Exemple de rezolvare a problemelor folosind proprietățile distribuției densității
Funcția de densitate de probabilitate este:
- Găsiți coeficientul de $ \ alpha $.
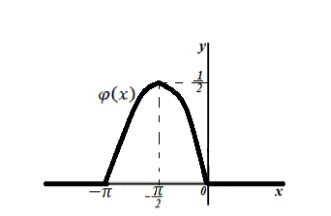
- Desenați graficul distribuției densității.
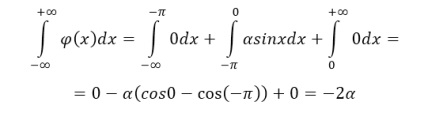
Folosind proprietatea 2, obținem:
Adică, funcția de densitate de distribuție este: