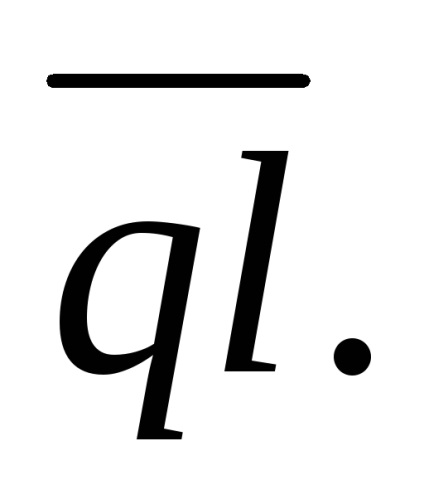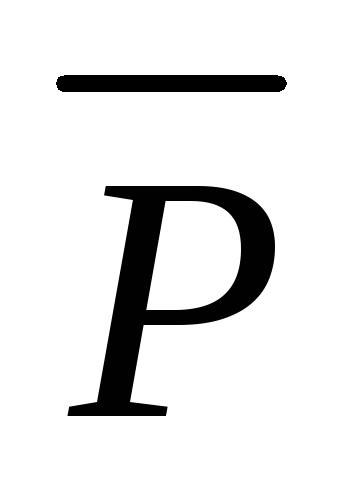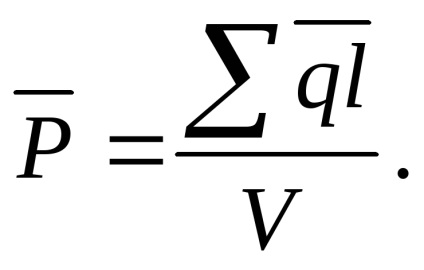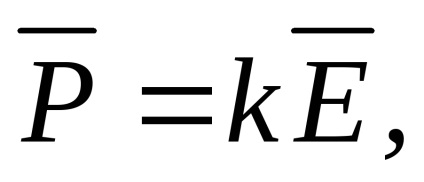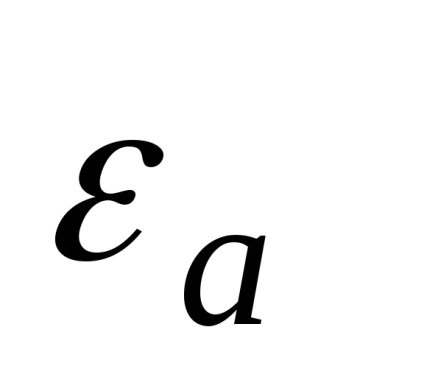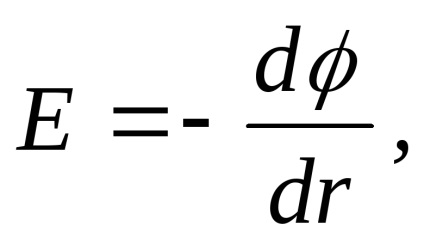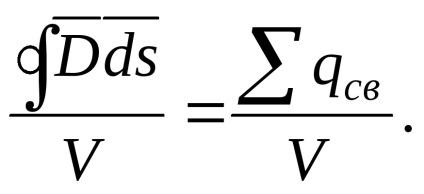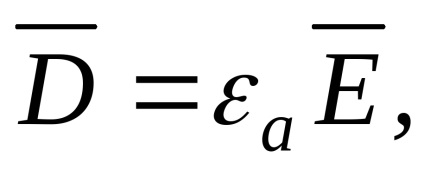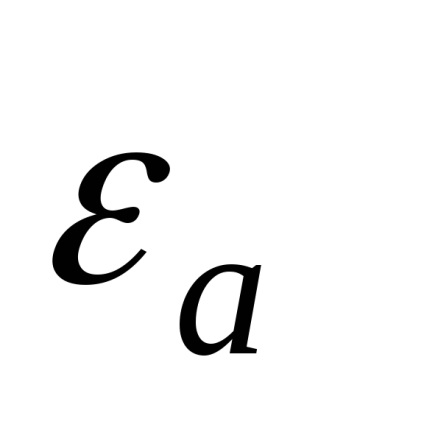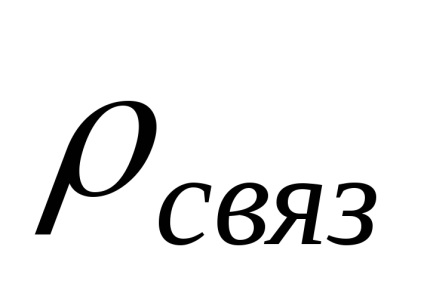În substanțe distinge între sarcini libere și legate. Timp liber sunt acele taxe care sub influența câmpului de forță se pot deplasa liber în substanța, mișcarea lor nu este restricționată de forțele intramoleculare. Sub cheltuieli legate realizeze astfel încât numai în interiorul moleculei poate fi deplasată sub influența intensitatea câmpului. taxele aferente nu pot fi separate de material astfel valoarea taxelor legate pozitive este suma negativ.
corpuri dielectrice sunt polarizate într-un câmp electrostatic. Prin polarizare a înțelege schimbarea ordonată a taxelor legate de amplasament de către forțele de câmp. Intuitiv, se poate demonstra folosind polarizarea ris.11.5, arătând corpul în absența câmpului electrostatic și dacă sunt disponibile. În cazul în care câmpul nu este prezent, atunci moleculele (dipolare) sunt situate în dezordine haotică (ris.11.5 la fel de bine). În același organism tarifele polarizate pozitive conectate sunt deplasate spre un potențial ridicat, și negativ - în direcția de mai mici (ris.11.5, b), în care shiftate, astfel încât puterea câmpului electric sunt echilibrate de forțe intramoleculare. Ca rezultat, polarizarea la suprafața expusă la substanțe ca sarcini pozitive sau negative sunt asociate cu suma primul dintre ele este exact egală cu a doua cantitate. Dipoli crea domeniul lor. Problema nepolarizată efectul lor cumulat este zero, iar în polarizat - nu, duce la o slăbire a câmpului rezultat și trebuie să fie luate în considerare. În acest scop, vom introduce conceptul de moment dipol electric. Două momentul electric egal în mărime și în semn opus taxelor deținute în afară de rasstoyaniil. Este produsul
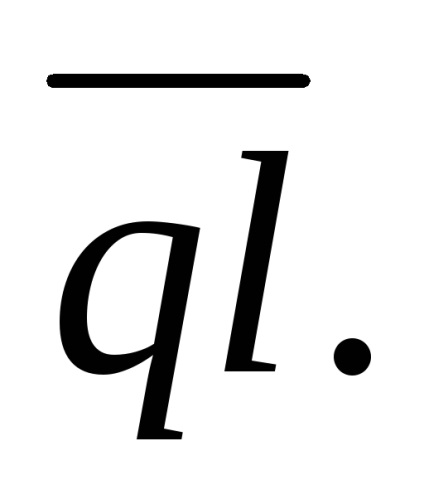
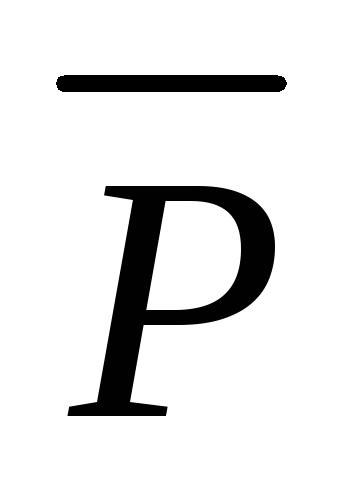
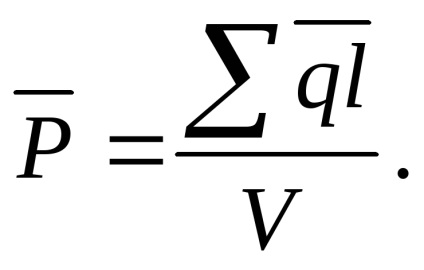
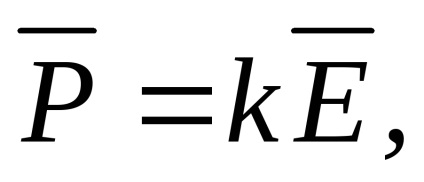
În plus față de cantitățile vectoriale de cele de mai sus
și, semnificație fizică pe care am găsit în teoria câmpului în calculul vectorului este introdus mai mult, numitul vector de deplasare electric sau vector de inducție electrică. Acesta este definit după cum urmează: în cazul în careSe numește constanta dielectrică relativă a mediului în care este creat și câmpulconstantă dielectrică absolută a mediului în care este creat câmpul.Acesta arată cât de multe ori proprietățile electrice ale mediului sunt diferite de proprietățile vidului (această diferență se produce din cauza polarizare). Pentru toate mass-mediaAcesta este determinat experimental și este dat în manuale.
teorema Gauss
Teorema lui Gauss este o lege de bază a câmpului electrostatic. Acesta este găsit experimental și matematic scris ca
flux vector de deplasare electric prin orice suprafață închisă care înconjoară un anumit volum este egal cu suma algebrică a taxelor libere, în interiorul suprafeței (în totaltaxele sunt luate cu semnele lor). ca. Pentru medii omogene și izotropeEste o constantă și poate fi luată în afara integral, atunciInteresant, fluxul vektoraD sau E depinde numai de și nu depinde de poziția taxei în interiorul suprafeței închise. Hraneste vektoraE a creat nu numai liber, dar, de asemenea, cheltuielile aferente. Acesta din urmă nu poate fi luată în considerare prin intermediul , și separat luate valoarea taxelor legate, iar apoi formula teorema lui Gauss este după cum urmează:Aceste trei formule sunt sub formă integrală înregistrare Gauss teorema, care, cu eficiență ridicată și simplitatea poate fi utilizat pentru calcularea intensității câmpului electromagnetic, în orice moment, dacă după ea poate efectua o suprafață închisă ale cărei puncte sunt în aceleași condiții, în ceea ce privește taxele, crearea unui câmp. Ca un exemplu, vom calcula câmpul produs de o sarcină punctiformă.
Un punct se numește o taxă situată pe corp este dimensiuni geometrice foarte mici. Pe ris.11.7 el este reprezentat de un punct (de unde și numele). Să presupunem că această sarcină este pozitiv și este situat într-un mediu cu constanta
. Ia-un punct arbitrar de pe rasstoyanier distanțată de la un punct de sarcină. Tensiunea la acest punct va fi direcționat de-a lungul unei linii radiale (vezi Fig. Ris.11.7). Pentru formula de calcul se aplică În acest scop, vom trage printr-un punct dat de o suprafață sferică închisă cu un centru de coincidentă cu un punct de încărcare. Vector suprafață elementarăîndreptate spre exterior normală la suprafață (situată în vecinătatea punctului în cauză). Deoarece în exemplu, vectori și DS noastre sunt aceleași, atunci produsul lor se potrivește cu modulele produsului. De asemenea, toate punctele acestei sfere valoarea vectorului E este aceeași cu simetrie. Acestea fiind spuse, avem de la suprafața sferei esteValoarea taxelor libere este dată doar o taxa de punct. Înlocuind aceste valori în formula de teorema lui Gauss, obținem:Astfel, această intensitate a câmpului variază invers proportsionalnor 2.
Capacitatea de calcul Proizvedom în acest domeniu, pe baza formulei
. Dacă luăm în considerare faptul că tensiunea și, în consecință, potențialul depinde doar de raza, acesta din urmă formula este rescris ca din aceasta rezultă că capacitatea în acest domeniu este invers proporțională cu r. Integrarea A constantă depinde în cazul în care pentru a localiza punctul de potențial zero.
Forma integrată a teoremei Gauss nu răspunde la întrebarea cum să contactați intensitatea câmpului la acel punct cu taxa de la acest punct. Răspunsul la această întrebare este furnizat de forma diferențială a acestei teoreme, care rezultă din integralei. Pentru această expresie
împărți cantitatea de volum limitat de integrare de suprafațăAceastă relație este valabilă pentru orice mărime de volum. L-am lăsa la zero (se spune că contractăm suprafața până la un punct). relație TogdaPredel vektoraD curgă printr-o suprafață închisă care mărginește un anumit volum, la valoarea acestui volum se numește divergența vectorului D () Sau sursă sau divergență. Pe partea dreaptă a ultima egalitate este un zaryadaρsv liber densitate în vrac. atunci Aceasta este legea lui Gauss în formă diferențială. Esența ei este explicată cu ajutorul a trei cazuri, reflectate pe ris.11.8. Dacă în punctul domeniu densitatea în vrac a considerat a taxei liber este pozitiv, atunci volumul infinitezimal care înconjoară un punct dat, linia vektoraD originea (sursa pozitivă, diferența este pozitivă, o divergență pozitivă). Dacă în punctul considerat al câmpului de densitate negativă gratuit de încărcare în vrac, volumul infinitezimal care înconjoară un anumit punct al liniei vectorului D include (o sursă negativă, diferența este negativă divergență negativă). Și, în sfârșit, în cazul în care punctul în cauză nu este gratuit, apoi la acel moment nu scurgere sau sursa liniilor vectoriale D. că într-un punct al liniei vectorului D nu începe și se termină, iar permeat volumul infinitezimal care înconjoară un punct dat.
ca
Pentru medii omogene și izotropeEste o constantă și poate fi luat în afara znakdiv. atunci obținem: Dacă se ia în considerare fenomenul de polarizare prin intermediul taxelor aferente, ultima expresie poate fi rescrisă cagdeρNe - densitatea în vrac a taxelor legate. Omiterea derivarea expresiei , scrie în sistemul de coordonate cartezieneea reprezintă parțial proeminențelor suma vektoraE a lungul a trei axe de coordonate. Arătăm că produsul scalar al operatorului NABLA și vectorul E este de a lua o abatere de la aceasta din urmă:
De aceea, teorema Gauss în formă diferențială este adesea scris ca
articole similare