linii paralele în spațiu
Două linii în spațiu numit paralel, dacă se află în același plan și nu se intersectează. Directe care nu se suprapun și nu se află în același plan, numit oblic (fig. 322).

Problema (3). Demonstrați că toate liniile care se intersectează două linii paralele date se află într-un singur plan.
Decizie. Deoarece liniile de date a și b sunt paralele, prin care se poate desena un plan (Fig. 323). Noi Denotă. Direct cu intersectând date linii paralele cu planul are și două puncte în comun - punctul de intersecție cu liniile de date. Prin Teorema 15.2, această linie se află în avion. Deci, toate liniile care se intersectează două linii paralele date se află într-un singur plan - planul.
Teorema 16.1. Printr-un punct în afara o anumită linie, puteți desena o linie dreaptă paralelă cu această linie, unul și numai unul.
Notă. Aprobarea unicitate Teorema 16.1 nu este o simplă consecință a axiomei paralel ca această axiomă afirmă unicitatea liniei paralel cu acest lucru în avion. Prin urmare, este nevoie de o dovadă.
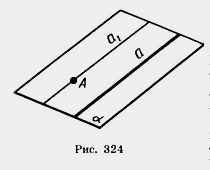
Dovada. Să o - dată linie dreaptă și un punct A care nu se află pe acea linie (Figura 324.). Printr-un punct A directă și planul. Prin punctul A, în planul liniei a1. paralel cu un. Demonstrați că a1. paralelă cu, este unic.
Să presupunem că există o altă linie dreaptă a2. care trece prin punctul A și o linie dreaptă paralelă cu un.
După o a2 directă și se poate realiza planul 2 plane 2 trece printr-o linie și punctul A; în consecință, prin Teorema coincide cu 15.1. Acum, prin axioma linii paralele și, și a2 sunt aceleași. Acest lucru dovedește teorema.
A. V. Pogorelov, Geometrie pentru clasele 7-11, manual pentru instituțiile de învățământ
Dacă aveți corecturi sau sugestii la această lecție, vă rugăm să ne contactați.
Dacă doriți să vedeți alte ajustări și sugestii pentru lecții, uita-te aici - Forumul Educațional.