Studierea fenomenelor naturii, rezolvarea diverselor sarcini în economie, biologie, fizica, inginerie, nu este întotdeauna posibil să se stabilească imediat o legătură directă între anumite valori de care descriu un anumit proces evolutiv. In general, se poate determina relația dintre aceste valori (funcții) și rata lor de schimbare în ceea ce privește cealaltă variabilă (independentă). Acest lucru ridică
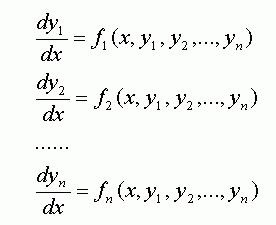
Ecuații diferențiale sunt:
1) Ecuația convențională order-I th, sunt integrate în piețe. Acestea, la rândul lor, sunt împărțite în: ecuații diferențiale cu variabile separabile; Controlul cu variabile separate; control uniform; controlul liniar; ecuații diferențiale exacte.
2) controlul de ordin superior.
3) Pentru Linear Control al II-lea, care sunt omogene de control liniar ordinul II-lea, cu coeficienți constanți și de control liniar neomogen cu coeficienți constanți.
Controlul de asemenea, rezolvată în mai multe moduri, dintre care cele mai frecvente - problema Cauchy, metodele lui Euler și Bernoulli, și altele.
În multe probleme de economie, matematică, tehnologia este necesară pentru a calcula un anumit număr de funcții care sunt asociate între ele o anumită cantitate de control. Apoi am ajuns la ajutorul sistemului de ecuații diferențiale: un set de ecuații, fiecare incluzând o variabilă independentă, funcția acestei independente și derivații acestora.
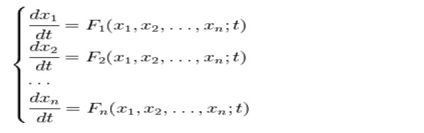
Dacă sistemul este liniar în funcțiile necunoscute, este numit un sistem liniar de ecuații diferențiale. Sistemul normal de ecuații diferențiale pot fi înlocuite cu un singur controler, din care ordinul este egal cu numărul de ecuații.
Sistemul de control al Conversion uneia ecuație, în unele cazuri, realizate prin utilizarea metodei de eliminare.
În plus față de toate cele de mai sus, există sisteme liniare cu coeficienți constanți, care pot fi ușor rezolvate prin metoda lui Euler.

