Evident că, în cazul în care distanța de la planul median mingea este egală cu raza planului, avionul atinge vasul de la un singur punct, iar aria secțiunii este zero, adică dacă b = R, atunci S = 0. Dacă b = 0, atunci cutplane Se trece prin centrul bilei. În acest caz, secțiunea transversală va fi un cerc, a cărui rază se potrivește cu raza de minge. Suprafața acestui cerc va fi, conform formulei este egală cu S = πR ^ 2.
Aceste două cazuri extreme furnizează granița dintre ele se va afla întotdeauna zona dorită: 0
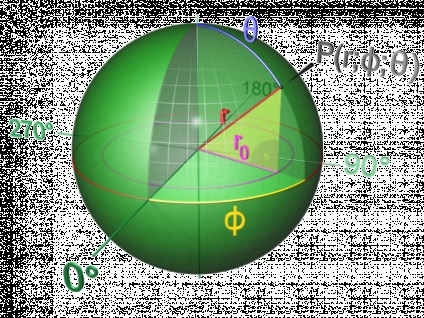
Deoarece distanța de la un punct la un plan este definit ca lungimea segmentului perpendicular pe planul și pornind de la un al doilea capăt al acestui picior coincide cu centrul circumferința secțiunii transversale. Această concluzie rezultă din definiția unei sfere: este evident că toate punctele aparțin circumferential aria secțiunii transversale și, prin urmare, se află la distanțe egale de centrul bilei. Aceasta înseamnă că fiecare punct al cercului secțională poate fi considerat ca vârful unui triunghi dreptunghic a cărui ipotenuză este raza de minge, unul dintre picioarele - perpendicular pe segmentul de linie care leagă centrul sferei cu planul, iar cea de a doua cateta - raza secțiunii transversale a cercului.
Dintre cele trei laturi ale triunghiului definit două - sferă cu raza R și distanța b, adică catete și ipotenuza. Lungimea pitagoreică a doua etapă să fie egală cu √ (R ^ 2 - b ^ 2). Aceasta este raza secțiunii cerc. Substituind valoarea găsită în formula de suprafață raza cercului, este ușor să tragem concluzia că zona secțiunii transversale a planului bilei este: S = π (R ^ 2 - b ^ 2) .În cazuri particulare în care b = R b = 0 sau dedus formula este în întregime în concordanță cu rezultatele deja găsite.
Toate planetele din sistemul solar au o formă sferică. În plus, sferică sau aproape de această formă și să aibă o mulțime de obiecte create de om, inclusiv detaliile tehnice ale dispozitivelor. Ball, ca orice rotire a corpului are o axă care coincide cu diametrul. Cu toate acestea, acest lucru nu este singura proprietate importantă a balonului. Următoarele sunt proprietățile de bază ale figuri geometrice și o cale de a găsi zona ei.
Dacă luați o jumătate de cerc sau de cerc și rotiți-l în jurul axei sale, pentru a obține corpul, numit o minge. Cu alte cuvinte, mingea este numit corp, o zonă limitată. Câmpul reprezintă coajă mingea. iar secțiunea transversală este un cerc. Din minge, aceasta diferă prin faptul că este gol. Axa ca cea a lumii. și domeniul de aplicare, la fel ca și diametrul și trece prin centrul. Raza segmentului sferic este numit, pus pe centrul său la orice punct extern. În zona de contrast, secțiunea bilei sunt cercuri. Forma aproape sferică, are majoritatea planetelor și corpurile cerești. La diferite puncte ale mingii sunt aceeași formă, dar inegale în mărime, secțiunea așa-numitele - cercuri de diferite dimensiuni.
Ball și sfera - corpul interschimbabil, spre deosebire de conul, în ciuda faptului că conul este, de asemenea, un corp de revoluție. Suprafața sferică este întotdeauna în secțiune transversală, pentru a forma un cerc, indiferent exact cum se rotește - orizontal sau vertical. Suprafața conică este obținută numai când se rotește triunghiul de-a lungul axei sale perpendicular pe substrat. Prin urmare con, spre deosebire de mingea. și nu este considerat organism interschimbabile de revoluție.
Cele mai mari cercuri posibile obținute prin bile secțiune plan care trece prin centrul O. Toate cercurile care trec prin centrul O, se intersectează într-un singur diametru. Raza este întotdeauna egală cu jumătate din diametrul. Două puncte A și B, care sunt situate oriunde în suprafața sferei. Este posibil să dureze un număr infinit de cercuri sau cercuri. Acesta este motivul pentru care un număr nelimitat de meridiane poate fi realizată prin polii Pământului.
Dacă găsiți zona mingea este considerată, mai presus de toate, zona poverhnosti.Ploschad mingii sferice. mai degrabă, sfera, care formează suprafața poate fi calculată pe baza ariei unui cerc cu aceeași R. raza Deoarece aria unui cerc este produsul razei semicerc, se poate calcula după cum urmează :? S = R ^ 2Tak atât prin centrul bilei sunt patru principale cerc mare, respectiv ploschadshara (sferă) este egal cu: S = 4 R ^ 2?
Această formulă poate fi utilă în cazul în care un diametru cunoscut sau raza sferei sau domeniul de aplicare. Totuși, acești parametri sunt prezentate ca nu toate problemele condiții geometrice. Există, de asemenea, probleme în care o minge înscrise într-un cilindru. În acest caz, utilizarea lui Arhimede teorema, esența care este faptul că suprafața bilei și jumătate ori mai mică decât suprafața totală a cilindrului: S = 2/3 S Cilindri. unde S cyl. este aria suprafeței totală a cilindrului.