
Acasă | Despre noi | feedback-ul
În primul rând, polinoamele Chebyshev au o astfel de proprietate importantă în cazul în care caracteristica statică elementul neliniar care este un polinom Cebîșev de grad n, se aplică un semnal armonic, de exemplu, cosinus (sinusoidală) a unității de amplitudine, ieșirea elementului neliniar de asemenea, va armonic semnal de unitate de amplitudine, dar cu o frecvență de n ori.
În al doilea rând, polinoamele Chebyshev cresc în afara intervalului [-1, 1] cel mai rapid din toate polinoame de același grad. Acestea sunt utilizate pentru sinteza filtrelor liniare [2]. Și un astfel de filtru la o undă predeterminată banda de trecere posedă caracteristica de frecvență cea mai abruptă într-un sistem de blocare bandă, în comparație cu alte filtre de același ordin.
În al treilea rând, polinoamele Chebyshev sunt stabilite ortogonale cu funcții de greutate [1], permițându-vă să ne imaginăm, de exemplu, caracteristica neliniară statică -non-unitate de timp unică întârziere în formă de rapid, mai degrabă convergente serie.
polinoamele Chebyshev sunt de forma [1, 2]:
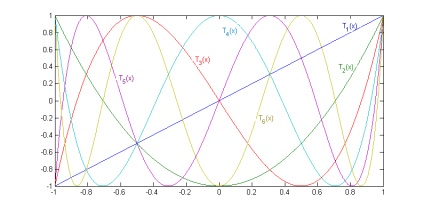
Graficele primele cinci polinoame Chebyshev sunt prezentate mai jos:
Fig. 1.1. polinoame Chebyshev. Cebîșev polinom peste intervalul (-1, 1) este limitată la valori (-1, 1), și în afara acestui interval creșteri în magnitudine mai rapid decât oricare alt polinom de același grad, limitată de aceeași condiție
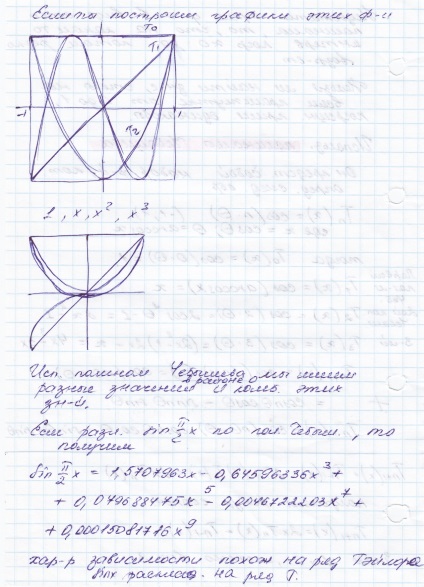
Când ai văzut prima polinoamele Chebyshev, apoi să acorde o atenție la prezentarea lor este:
că, la prima vedere mod de neînțeles, dar legături foarte frumos trigonometria si algebra.
polinoame Chebyshev de primul tip sunt funcții ortogonale ale sistemului și sunt definite după cum urmează:
Folosind relația pentru sumele trigonomitricheskie cosinus și diferențele pot fi afișate pentru a găsi recurență polinoame Chebyshev:
Polinomul Tn (x) este cuprins în intervalul [-1,1] exact n rădăcini situate la punctele
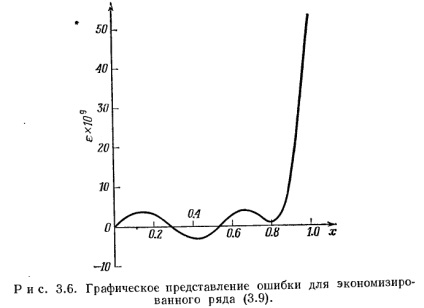
Orice functie f (x), definită pe intervalul [-1,1] poate fi aproximată prin următoarea formulă:






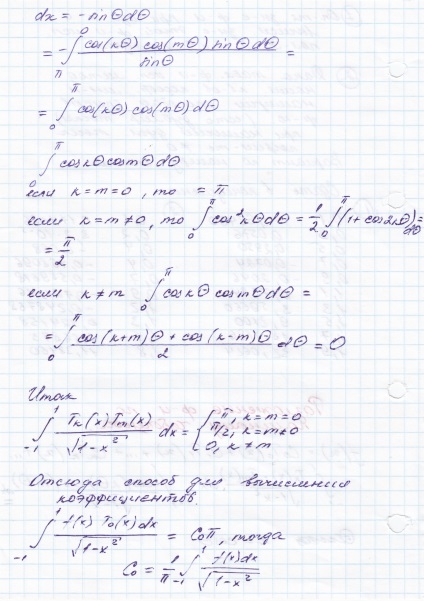

Introducere și funcții raționale fracție continuă










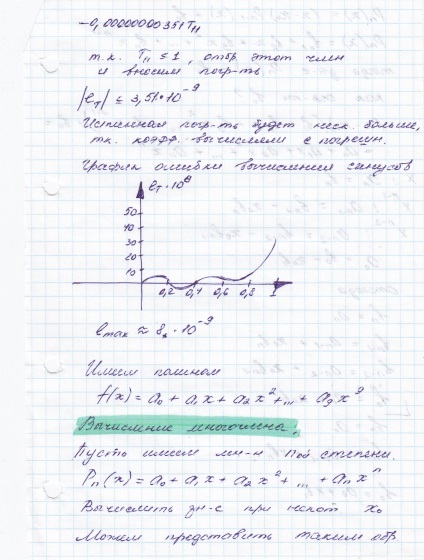
Schema de calcul polinomul Horner
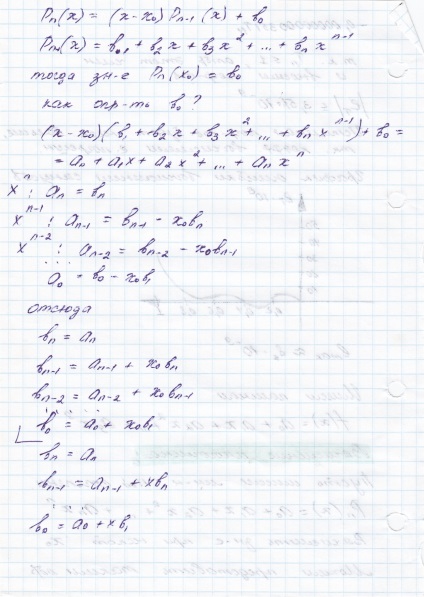
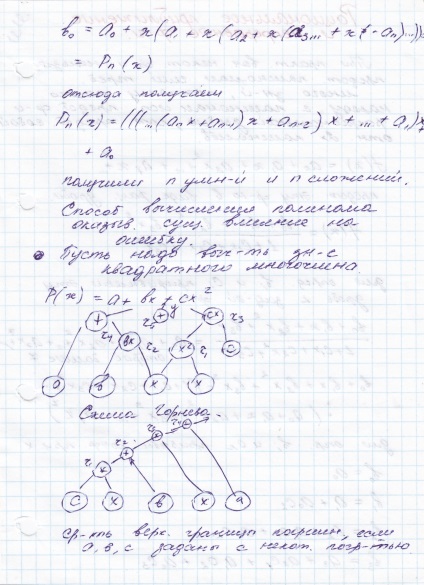




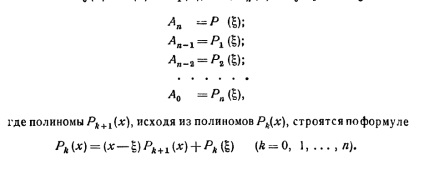


Limitele tuturor rădăcinilor polinomului
Limitele rădăcinile reale ale polinomului







Metode de clarificare a rădăcinilor reale ale ecuațiilor neliniare (jumătate și diviziunea proporțională, Newton, combinate, iterativ, usov.iteteratsii). condiție pentru convergența metodelor iterative.



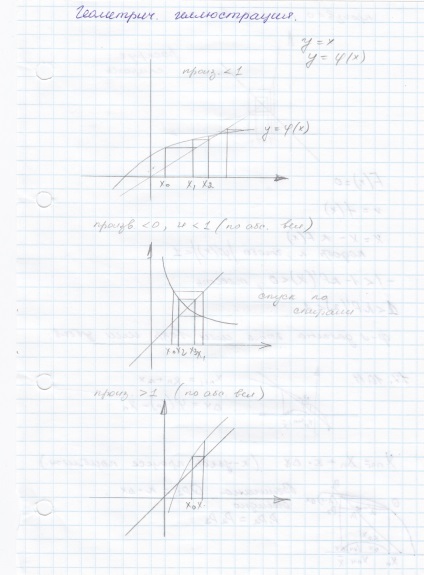



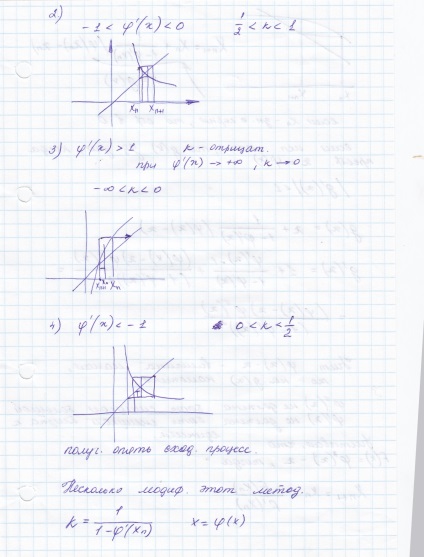




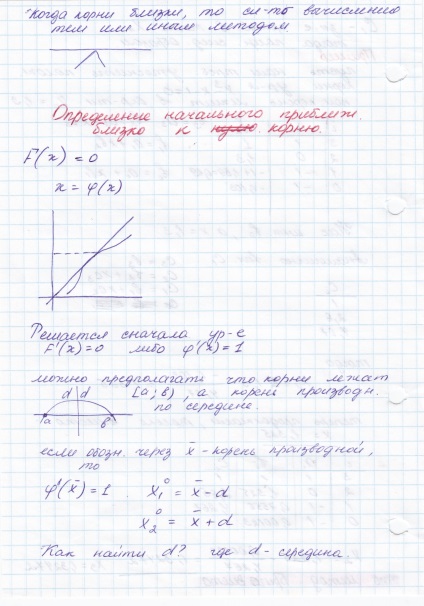
Găsirea valorile inițiale apropiate de zero, polinomul


15. Metoda Vietti Brig-13 =