2 Ce este Pyramid Pyramid - o figură geometrică, care constă dintr-un poligon, punctul nu se află în planul poligonului și toate segmentele de legătură cu acest punct punctele de poligon.

3 piramidă înălțimea structurii apotemă de fețele laterale piramidă regulată trasată de la nodurile sale; fețe laterale triunghiuri care converg la vârf; coaste laterale laterale comune ale fețelor laterale; punct piramida vertex, care leagă marginile laterale și situată într-un plan de bază; înălțimea segmentului perpendicular trasată prin vârful piramidei pe planul său de bază (capetele acestui segment sunt vertex piramidă și suprafața normală); secțiunea diagonală a piramidei secțiunii piramidei, extinzându-se prin partea superioară și baza diagonală; poligon de bază, care nu face parte din vârful piramidei.

4
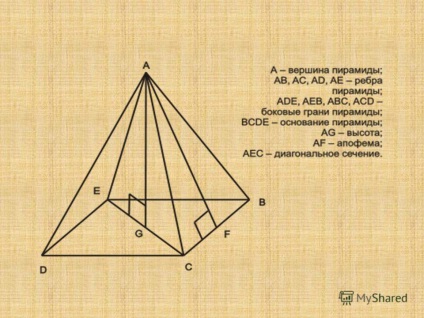
6 corectă Pyramid Piramida se numește regulat în cazul în care baza sa este un poligon regulat și vârful proiectat în centrul bazei. marginile laterale ale piramidei sunt corecte; în fețele laterale dreapta ale piramidei toate triunghiuri isoscele; orice piramidă regulată poate scrie atât și să descrie domeniul de aplicare în jurul acestuia; zona din dreapta suprafață laterală a piramidei este jumătate din produsul din perimetrul bazei pe apofemu. Proprietăți piramidă regulată.

7 O piramidă piramidă dreptunghiulară numită dreptunghiulară, dacă una dintre marginile laterale ale piramidei perpendicular pe bază. În acest caz, este marginea și înălțimea piramidei.
8 piramidă trunchiată un trunchi de piramidă se numește poliedru, închisă între baza piramidei și un plan secant paralel cu baza sa.
9 Proprietăți piramide Dacă toate muchiile laterale sunt egale, atunci: în partea de jos a piramidei poate fi descrisă ca un cerc, cu vârful piramidei este proiectată în centrul său; coaste laterale formează cu planul de bază unghiuri egale. Reversul este valabil, de exemplu, dacă marginile laterale formează un plan de bază unghiuri egale, sau dacă este aproape de baza piramidei poate fi descrisă ca un cerc, cu vârful piramidei este proiectată în centrul ei, atunci toate marginile laterale ale piramidei sunt egale. În cazul în care fețele laterale sunt înclinate față de planul bazei la un unghi, apoi: la baza piramidei, puteți înscrie într-un cerc, cu partea de sus a piramidei este proiectată în centrul său; înălțimea fețelor laterale sunt egale; suprafață laterală egală cu jumătate din perimetrul produsului de bază la o înălțime a feței laterale.
10 Teorema Teorema Dacă toate fețele laterale ale piramidei sunt la fel înclinate în raport cu planul bazei și se extinde în interiorul înălțimea piramidei, înălțimea trece prin centrul cercului înscris în baza piramidei. Teorema Dacă toate fețele laterale sunt înclinate față de planul de bază la același unghi, că această formulă este valabilă, în special, pentru piramida regulate.
Formula 11 asociat cu volumul piramidei piramidei poate fi calculată cu formula: în care S amprenta la sol și la înălțime; unde h este volumul cutiei; De asemenea, volumul piramidei triunghiulare (tetraedru) poate fi calculată conform formulei. Acolo unde coastele înclinării, distanța și unghiul dintre și; Este suma suprafața totală a suprafeței laterale și suprafața de bază: Pentru a determina suprafața laterală a unei piramide drept poate folosi formula:
12 Exemple de rezolvare a problemelor este dat. La regulate patrulateră piramidă SABCD centrul de bază punct O, S vertex, SO = 51, AC = 136. Găsit margine laterală SC. Soluție: SOC: rectangel, unghi SOC = 90 grade
13 Având în vedere: la intervale regulate de piramidă triunghiulară SABC R la mijlocul coaste BC, S vârf. Este cunoscut faptul că AB = 7 și SR = 16. Găsit: suprafața laterală. Soluție: 1) Suprafața suprafeței laterale a unei piramide triunghiulare regulate este egală cu jumătate din produsul din perimetrul bazei la apofemu (apotemă este înălțimea feței laterale a unei piramide regulate realizată din vârful său): 2) sau se poate spune că suprafața laterală a piramidei este suma suprafețelor din trei fețe laterale. Marginile laterale într-o piramidă triunghiulară regulată sunt egale în triunghiuri zona. În acest caz: