Legile Kirchhoff stabilesc relații între curenți și tensiuni în circuitele electrice ramificați de tip arbitrar. Legile lui Kirchhoff sunt de o importanță deosebită în domeniul ingineriei electrice, datorită versatilității sale, ca fiind adecvat pentru a rezolva orice probleme electrice.
Prima lege Kirchhoff rezultă din legea conservării taxa. Aceasta constă în faptul că suma algebrică a curenților de la orice nod convergentă este zero.
în care: - numărul de curenți care converg la acest nod. (. Figura 1) De exemplu, pentru un ansamblu de circuit electric, ecuația primei legi a lui Kirchhoff poate fi scris ca I1 - I2 + I3 - I4 + I5 = 0
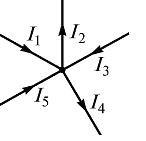
În această ecuație, curenții îndreptate spre nodul luate pozitiv.
A doua lege a lui Kirchhoff: suma algebrică a căderilor de tensiune de la site-urile selectate în buclă închisă selectată arbitrar în lanț ramificat complex, egal cu suma algebrică a tensiunii în acest circuit
unde k - numărul surselor CEM; m - numărul de sucursale într-o buclă închisă; Ii. Ri - rezistență și curent i-lea ramură.
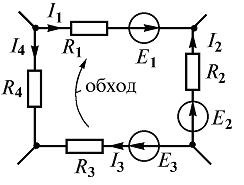
Deci, pentru un circuit în buclă închisă (figura 2) E1 -. E2 + E3 = I1R1 - I2R2 + I3R3 - I4R4
Notă despre semnele ecuației care rezultă:
1) EMF pozitiv dacă direcția coincide cu direcția circuitului de bypass selectat arbitrar;
2) căderea de tensiune pe rezistor este pozitiv în cazul în care direcția de curent în ea coincide cu direcția de traversal.
Calculul circuitului electric ramificat folosind legile lui Kirchhoff
Metoda constă în compilarea ecuații din prima și a doua legile Kirchhoff în circuitul nodurilor și contur și rezolvarea acestor ecuații pentru a determina curenții necunoscuți în ramuri și pe ele - tensiuni. Prin urmare, numărul de necunoscute este egal cu numărul de sucursale b. prin urmare, același număr de ecuații independente este necesară pentru a face prima și a doua legile Kirchhoff.
Numărul de ecuații care pot fi derivate din prima lege este egal cu numărul de noduri de circuit, și numai (y - 1) ecuații sunt independente unul față de celălalt.
independență ecuații este asigurată prin selectarea nodurilor. Nodurile sunt în mod obișnuit selectați astfel încât fiecare nod succesive este diferit de nodurile adiacente cel puțin o ramură. Ecuațiile rămase sunt făcute de-a doua lege a lui Kirchhoff a circuitelor independente, adică numărul de ecuații b - (y - 1) = b - y +1.
Contur este numit independent, în cazul în care conține cel puțin o ramură, care nu sunt incluse în alte circuite.
Kirchhoff formează ecuațiile pentru circuitul (Fig. 3). Circuitul cuprinde patru noduri și șase ramuri.
Prin urmare, în conformitate cu prima lege a Kirchhoff compune y - 1 = 4 - 1 = 3 ecuație, iar al doilea b - y + 1 = 6 - 4 + 1 = 3. De asemenea, cele trei ecuații.
alege în mod arbitrar o direcție pozitivă curentă în toate ramurile (fig. 4). circuite ocolesc direcția vom alege în sensul acelor de ceasornic.
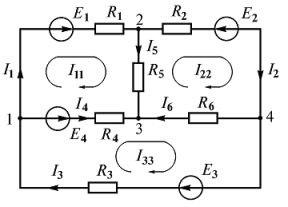
Facem până la numărul necesar de ecuații de prima și a doua legi ale Kirchhoff
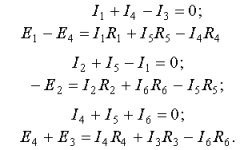
Sistemul de ecuații rezultat este rezolvat pentru curenți. În cazul în care calculul curentului în ramura a apelat la minus, atunci direcția este opusă direcției adoptate.
Legile lui Kirchhoff în formă complexă
Pentru circuite cu legile sinusoidale actuale Kirchhoff sunt formulate în același mod ca și pentru circuitul de curent continuu, dar numai la valorile complexe ale curenților și tensiunilor.
Prima lege a Kirchhoff. „Algebrică suma complexelor nodului curent în circuit este zero“
A doua lege a Kirchhoff. „În orice circuit buclă închisă suma algebrică integrată a electromotoare egală cu suma algebrică a tensiunilor complexe la toate elementele pasive ale acestui circuit.“