

Să considerăm un exemplu. Suma inițială în contul bancar este de $ 1000, și o rată cumulativă anuală a dobânzii este de 3%. Se înregistrează funcția exponențială care descrie procesul de acumulare de pe acest cont.
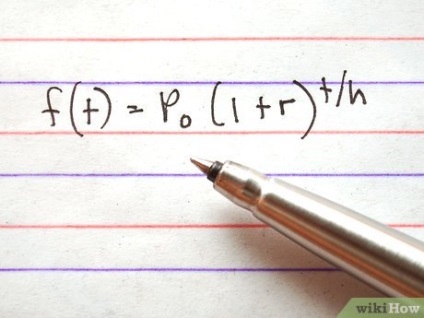
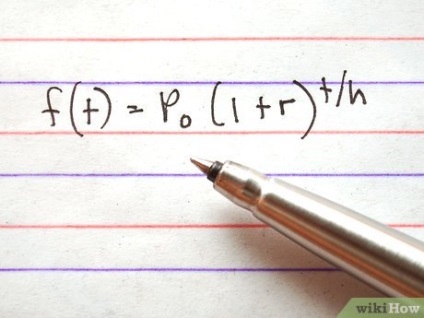
Forma de bază a funcției exponențiale - f (t) = P (1 + r) t / h. unde P0 - valoarea inițială, t - variabila timp, r - rata dobânzii, h - numărul de perioade de timp (t variabilă).


Valoarea caracteristică pentru a substitui o valoare P r inițială și rata dobânzii. Vei primi o funcție de forma: f (t) = 1000 (1,03) t / h.
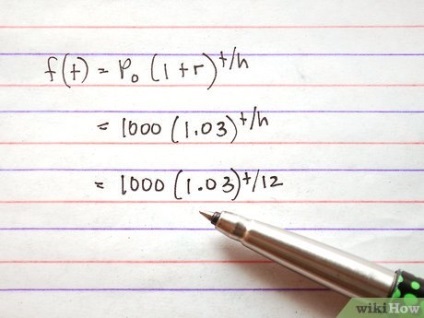
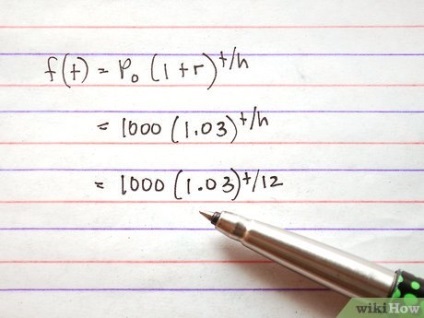
Găsiți h. În fiecare an, contribuția este a crescut cu 3%, adică a crescut cu 3%, la fiecare 12 luni. Din moment ce trebuie să-și exprime în T luni, trebuie să împartă cu 12 t; deci, t = 12. Primesti funcție de forma: f (t) = 1,000 (1,03) t / 12.
Metoda 2 din 2:
Utilizarea „e“ ca nivel de bază Edit


Definiții. „E“ - este o constantă matematică (numărul lui Euler), este aproximativ egal cu 2,72. Funcția exponențiale, care acționează ca bază „e“ se numește o funcție exponențială.


Să considerăm un exemplu. izotop de carbon timp de înjumătățire este de 50 de ani. (Timp de înjumătățire a -. Timpul în care este redusă la jumătate numărul de nuclee radioactive) Se înregistrează funcția exponențială care descrie procesul de descompunere a 500 g de izotop de carbon.


Forma de bază a funcției exponențiale - f (t) = ae kt. și în care - valoarea inițială, e - numărul Euler, k - factorul de proporționalitate unele, t - variabila timp.


Membru supleant valoarea valoarea inițială. Vei primi o funcție de forma: f (t) = 500E kt.
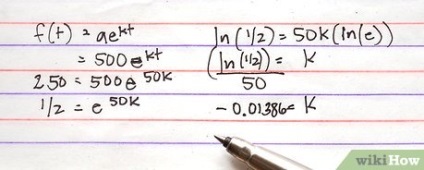
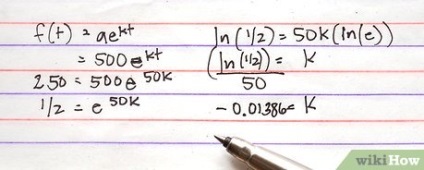
Găsiți coeficientul de proporționalitate. El caracterizează rata de schimbare a graficului funcției. Știți că în 50 de ani va fi de 250 de grame de izotop de carbon. Adică, dacă t = 50, atunci f (50) = 250. supleant aceste valori în funcție, înregistrare ecuație exponențială și rezolva: 250 = 500e 50k. În primul rând, împărțiți ambele părți de 500 și veți obține: 1/2 = e 50k. Acum, ia logaritmul natural al ambelor părți ale ecuației: ln (1/2) = 50k (ln (e)) (în conformitate cu proprietățile logaritmilor, logaritmul argumentului index poate fi luat ca un semn al logaritmului, adică, ln e 50k = 50k (ln (e)) ). Mai mult, în conformitate cu proprietățile logaritmilor, logaritmul argumentului, și egală cu baza este 1, adică ln e = 1. Astfel, ecuația se simplifică la: ln (1/2) = 50k și k = (ln (1/2)) / 50 ≈ -0,01386. Vă rugăm să rețineți că aceasta este o valoare negativă. În cazul în care un coeficient negativ, această funcție scade; în caz contrar, funcția crește.
Membru supleant valoarea lui k. Forma finală a funcției:- f (t) = 500e -0,01386t.
Regulamentul
- Pentru a obține valori exacte ale funcției pentru a salva valoarea lui k în calculator (valoarea exactă și nu rotunjite). Atunci când reprezentarea grafică a nu confunda variabila independentă - în exemplele descrise mai este denumit «T».
- Vei învăța cum să determine rapid situația corespunzătoare uneia dintre funcțiile de mai sus. De obicei, problema este mai ușor de rezolvat, folosind prima funcție, dar sunt momente când este necesar să se utilizeze o funcție exponențială.
articole suplimentare


Cum se convertesc la mililitri de grame
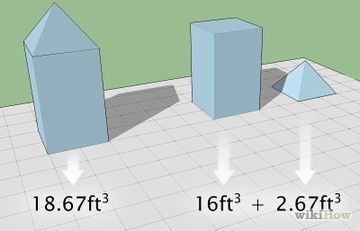

Cum se calculează volumul cutiei
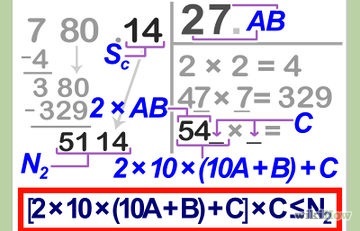

Cum de a găsi rădăcina pătrată a unui număr manual

Cum de a calcula probabilitatea


Cum se calculează variația procentuală


Cum de a calcula rata de creștere


Cum de a găsi domeniul funcției
Cum de a simplifica expresii algebrice


Cum de a găsi un set de valori
Traducerea din zecimal în binar